
)設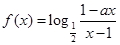 為奇函數,
為奇函數,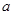 為常數.
為常數.
(1)求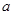 的值;
的值;
(2)判斷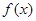 在區間(1,+∞)內的單調性,并證明你的判斷正確;
在區間(1,+∞)內的單調性,并證明你的判斷正確;
(3)若對于區間 [3,4]上的每一個 的值,不等式
的值,不等式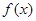 >
>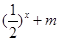 恒成立,求實數
恒成立,求實數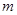 的取值范圍.
的取值范圍.
(1)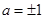 (2)在(1,+∞)上是增函數(3)
(2)在(1,+∞)上是增函數(3)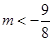
【解析】
試題分析:解:(1)∵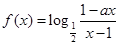 為奇函數,
為奇函數,
∴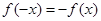 對于
對于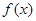 定義域中任意實數恒成立,
定義域中任意實數恒成立,
即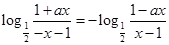 2分
2分
∴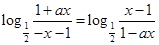 ∴
∴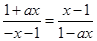 ∴
∴
∴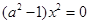 對于
對于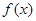 定義域中任意實數恒成立
定義域中任意實數恒成立
∵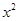 不恒為0,∴
不恒為0,∴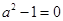 ∴
∴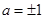 4分
4分
當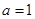 時
時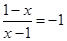 不符題意
不符題意
∴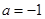 5分
5分
(2)由(1)得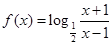
設1<x1<x2,則
f(x1)-f(x2)=log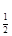
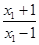 -log
-log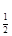
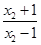 =log
=log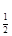
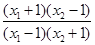
=log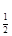
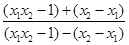 7分
7分
∵ 1<x1<x2,∴ x2-x1>0,
∴ (x1x2-1)+(x2-x1)>(x1x2-1)-(x2-x1)>0
即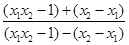 >1. 9分
>1. 9分
∴ f(x1)-f(x2)<0即f(x1)<f(x2),在(1,+∞)上是增函數 10分
(3)由(1),不等式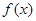 >
>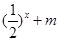 可化為
可化為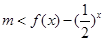 ,即
,即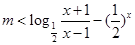
由題意得對于區間[3,4]上的每一個 的值,
的值,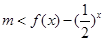 恒成立 2分
恒成立 2分
令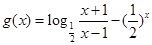 ,則
,則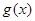 區間[3,4]上為增函數
區間[3,4]上為增函數
∵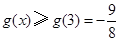 ∴
∴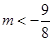 15分
15分
考點:函數性質的綜合運用
點評:解決的關鍵是對于函數奇偶性和單調性的靈活運用,以及利用分離參數的思想求解函數的最值得到范圍。屬于中檔題。


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:高中數學 來源: 題型:
(09年山東蒼山期末文)(14分)設![]() 為奇函數,
為奇函數,![]() 為常數。
為常數。
(1)求![]() 的值;
的值;
(2)證明:![]() 在(1,+∞)內單調遞增;
在(1,+∞)內單調遞增;
(3)若對于[3,4]上的每一個![]() 的值,不等式
的值,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
設![]() 為奇函數,
為奇函數,![]() 為常數.
為常數.
(1)求![]() 的值;
的值;
(2)證明![]() 在區間(1,+∞)內單調遞增;
在區間(1,+∞)內單調遞增;
(3) 若對于區間[3,4]上的每一個![]() 的值,不等式
的值,不等式![]() >
>![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014屆天津市、漢沽一中高一上學期期末聯考數學試卷 題型:解答題
設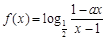 為奇函數,
為奇函數,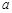 為常數.
為常數.
(Ⅰ)求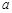 的值; (Ⅱ)判斷
的值; (Ⅱ)判斷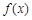 在區間(1,+∞)的單調性,并說明理由;
在區間(1,+∞)的單調性,并說明理由;
(Ⅲ)若對于區間[3,4]上的每一個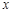 值,不等式
值,不等式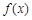 >
>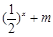 恒成立,求實數
恒成立,求實數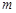 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013屆云南省高二上學期期末考試理科數學試卷 題型:解答題
(12分)設 為奇函數,
為奇函數,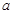 為常數。
為常數。
(1)求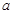 的值;
的值;
(2)證明: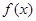 在(1,+∞)內單調遞增;
在(1,+∞)內單調遞增;
(3)若對于[3,4]上的每一個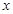 的值,不等式
的值,不等式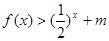 恒成立,求實數
恒成立,求實數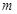 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com