
【題目】已知函數![]() ,
,![]() ,
,![]() .
.
(1)求函數![]() 的極值點;
的極值點;
(2)已知T(![]() ,
,![]() )為函數
)為函數![]() ,
,![]() 的公共點,且函數
的公共點,且函數![]() ,
,![]() 在點T處的切線相同,求a的值;
在點T處的切線相同,求a的值;
(3)若函數![]() 在(0,
在(0,![]() )上的零點個數為2,求a的取值范圍.
)上的零點個數為2,求a的取值范圍.
【答案】(1)![]() (2)a = e. (3)a > e.
(2)a = e. (3)a > e.
【解析】
(1)對函數求導,得到導函數的零點和在零點兩側的單調性,進而得到極值點;(2)點T(x0,y0)為函數![]() ,
,![]() 的公共點,且函數
的公共點,且函數![]() ,
,![]() 在點T處的切線相同,所以
在點T處的切線相同,所以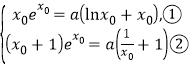 且
且![]() ,聯立兩式消參得到
,聯立兩式消參得到![]() ,從而求出零點,進而得到參數值;(3)設函數
,從而求出零點,進而得到參數值;(3)設函數![]() ,
,![]() .則
.則![]() ,令
,令![]() 得,
得,![]() ,
,![]() 函數單調故不可能有2個零點,結合函數單調性證明a > e時有2個零點即可.
函數單調故不可能有2個零點,結合函數單調性證明a > e時有2個零點即可.
(1)因為![]() ,所以
,所以![]() .
.
令![]() 得,x = -1,
得,x = -1,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以函數![]() 的極小值點為x = -1,不存在極大值點.
的極小值點為x = -1,不存在極大值點.
(2)依題意![]() .
.
因為點T(x0,y0)為函數![]() ,
,![]() 的公共點,且函數
的公共點,且函數![]() ,
,![]() 在點T處的切線相同.
在點T處的切線相同.
所以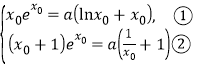 且
且![]() ,
,
由②得,![]() ,代入①得,
,代入①得,![]() ,顯然
,顯然![]() ,
,
所以![]() .
.
因為![]() 滿足該方程,且函數
滿足該方程,且函數![]() 為單調增函數,所 以,
為單調增函數,所 以,![]() ,a = e.
,a = e.
(3)設函數![]() ,
,![]() .
.
則![]() ,
,
令![]() 得,
得,![]() .
.
當![]() 時,
時,![]() ,所以
,所以![]() 為(0,+
為(0,+![]() )上單調增函數,至多1個零點,不符,舍去;
)上單調增函數,至多1個零點,不符,舍去;
當a > 0時,![]() 得,
得,![]() ,由(1)知,
,由(1)知,![]() 為(-1,+
為(-1,+![]() )上單調增函數,所以
)上單調增函數,所以![]() 在(0,+
在(0,+)上有唯一解,記為
![]() , 即
, 即![]() 的根為
的根為![]() .
.
當![]() 時,
時,![]() ,單調遞減
,單調遞減![]() ;
;
當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
因為函數![]() 的零點個數為2.
的零點個數為2.
下證:a > e時,函數![]() 在(0,+
在(0,+![]() )上的零點個數為2.
)上的零點個數為2.
因為![]() ,
,
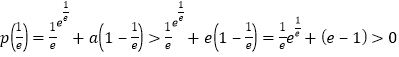 ,
,
![]() ,
,
根據![]() 的單調性結合零點存在性定理知,函數
的單調性結合零點存在性定理知,函數![]() 在(
在(![]() ,x1)上存在一個零點,在(x1,2a)上存在一個零點,故函數
,x1)上存在一個零點,在(x1,2a)上存在一個零點,故函數![]() 在(0,+
在(0,+![]() )上的零點個數為2.
)上的零點個數為2.
所以a > e.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex+e-x,g(x)=2x+ax3,a為實常數.
(1)求g(x)的單調區間;
(2)當a=-1時,證明:存在x0∈(0,1),使得y=f(x)和y=g(x)的圖象在x=x0處的切線互相平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將參加夏令營的400名學生編號為:001,002,…,400,采用系統抽樣的方法抽取一個容量為40的樣本,且隨機抽得的號碼為003,這400名學生分住在三個營區,從001到180在第一營區,從181到295在第二營區,從296到400在第三營區,三個營區被抽中的人數分別為( )
A. 18,12,10 B. 20,12,8 C. 17,13,10 D. 18,11,11
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某群體的人均通勤時間,是指單日內該群體中成員從居住地到工作地的平均用時.某地上班族![]() 中的成員僅以自駕或公交方式通勤.分析顯示:當
中的成員僅以自駕或公交方式通勤.分析顯示:當![]() 中
中![]() (
(![]() )的成員自駕時,自駕群體的人均通勤時間為
)的成員自駕時,自駕群體的人均通勤時間為 (單位:分鐘),而公交群體的人均通勤時間不受
(單位:分鐘),而公交群體的人均通勤時間不受![]() 影響,恒為
影響,恒為![]() 分鐘,試根據上述分析結果回答下列問題:
分鐘,試根據上述分析結果回答下列問題:
(1)當![]() 在什么范圍內時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
在什么范圍內時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
(2)求該地上班族![]() 的人均通勤時間
的人均通勤時間![]() 的表達式;討論
的表達式;討論![]() 的單調性,并說明其實際意義.
的單調性,并說明其實際意義.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廠家在產品出廠前,需對產品做檢驗,廠家將一批產品發給商家時,商家按合同規定也需隨機抽取一定數量的產品做檢驗,以決定是否接收這批產品.
(1)若廠家庫房中(視為數量足夠多)的每件產品合格的概率為 ![]() 從中任意取出 3件進行檢驗,求至少有
從中任意取出 3件進行檢驗,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若廠家發給商家![]() 件產品,其中有
件產品,其中有![]() 不合格,按合同規定 商家從這
不合格,按合同規定 商家從這![]() 件產品中任取
件產品中任取![]() 件,都進行檢驗,只有
件,都進行檢驗,只有![]() 件都合格時才接收這批產品,否則拒收.求該商家可能檢驗出的不合格產品的件數ξ的分布列,并求該商家拒收這批產品的概率.
件都合格時才接收這批產品,否則拒收.求該商家可能檢驗出的不合格產品的件數ξ的分布列,并求該商家拒收這批產品的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國有悠久的金石文化,印信是金石文化的代表之一.印信的形狀多為長方體、正方體或圓柱體,但南北朝時期的官員獨孤信的印信形狀是“半正多面體”(圖1).半正多面體是由兩種或兩種以上的正多邊形圍成的多面體.半正多面體體現了數學的對稱美.圖2是一個棱數為48的半正多面體,它的所有頂點都在同一個正方體的表面上,且此正方體的棱長為1.則該半正多面體共有________個面,其棱長為_________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司將進的一批單價為7元的商品,若按單價為10元銷售,每天可以賣出100個,若每個商品的銷售價上漲1元,則每天的銷售量就減少10個.
(1)設每個商品的銷售價上漲![]() 元,每天的利潤為
元,每天的利潤為![]() 元,試寫出函數關系式.
元,試寫出函數關系式.
(2)當每個商品的銷售價定為多少時,每天的利潤達到最大?并求出最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com