【題目】已知數(shù)列{an}的前n項和Sn＝1+λan，其中λ≠0．
（1）證明{an}是等比數(shù)列，并求其通項公式；
（2）當λ＝2時，求數(shù)列{
}的前n項和．
【答案】(1)證明見解析 ，an
(2)
1．
【解析】
（1）數(shù)列{an}的前n項和Sn＝1+λan，其中λ≠0．n＝1時，a1＝1+λa1，λ≠1，解得a1．n≥2時，an＝Sn﹣Sn﹣1，化為：
．即可證明{an}是等比數(shù)列，進而得出其通項公式．
（2）當λ＝2時，an＝﹣2n﹣1．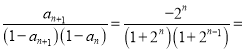
2
．利用裂項求和方法即可得出．
（1）證明：數(shù)列{an}的前n項和Sn＝1+λan，其中λ≠0．
n＝1時，a1＝1+λa1，λ≠1，解得a1．
n≥2時，an＝Sn﹣Sn﹣1＝1+λan﹣（1+λan﹣1），化為：
．
∴數(shù)列{an}是等比數(shù)列，首項為
，公比為：
．
∴an，
（2）解：當λ＝2時，an＝﹣2n﹣1．
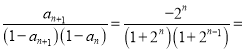2．
∴數(shù)列{
}的前n項和＝2[
＝2（
）
1．
鷹派教輔銜接教材河北教育出版社系列答案
初中暑期銜接系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知極點與坐標原點
重合，極軸與
軸非負半軸重合，
是曲線
上任一點
滿足
，設點的軌跡為
.
（1）求曲線的平面直角坐標方程；
（2）將曲線向右平移
個單位后得到曲線
，設曲線與直線
（
為參數(shù)）相交于
、
兩點，記點
，求
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下列命題:
①關于
、
的二元一次方程組
的系數(shù)行列式
是該方程組有解的必要非充分條件;
②已知
、
、
、
是空間四點,命題甲:、、、四點不共面,命題乙:直線
和
不相交,則甲成立是乙成立的充分非必要條件;
③“
”是“對任意的實數(shù),
恒成立”的充要條件;
④“
或
”是“關于的方程
有且僅有一個實根”的充要條件;
其中,真命題序號是________
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
（a為常數(shù)）與x軸有唯一的公共點A．
（Ⅰ）求函數(shù)
的單調(diào)區(qū)間；
（Ⅱ）曲線在點A處的切線斜率為
，若存在不相等的正實數(shù)
，
，滿足
，證明：
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖所示，四棱錐
底面是直角梯形，點E是棱PC的中點，
，
底面ABCD，
.
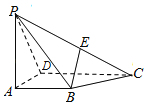
（1）判斷BE與平面PAD是否平行，證明你的結論；
（2）證明：
平面
；
（3）求三棱錐
的體積V.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】至
年底，我國發(fā)明專利申請量已經(jīng)連續(xù)
年位居世界首位，下表是我國
年至年發(fā)明專利申請量以及相關數(shù)據(jù).
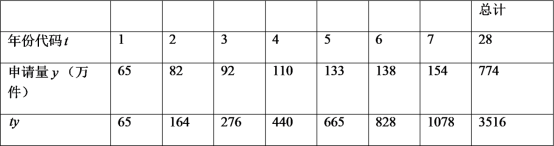
注：年份代碼
～
分別表示～.
（1）可以看出申請量每年都在增加，請問這幾年中哪一年的增長率達到最高，最高是多少？
（2）建立
關于
的回歸直線方程（精確到
），并預測我國發(fā)明專利申請量突破
萬件的年份.
參考公式：回歸直線的斜率和截距的最小二乘法估計分別為
，
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在如圖所示的幾何體中，四邊形ABCD是正方形，PA⊥平面ABCD，E，F分別是線段AD，PB的中點，PA＝AB＝1.
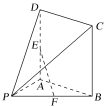
(1)證明：EF∥平面PDC；
(2)求點F到平面PDC的距離.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系xOy中，曲線
的參數(shù)方程為
（
，
為參數(shù)），曲線上的點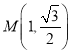
對應的參數(shù)
．在以O為極點，x軸的正半軸為極軸的極坐標系中，曲線
是圓心在極軸上，且經(jīng)過極點的圓．射線
與曲線交于點
．
（1）求曲線的直角坐標方程；
（2）若點
，
在曲線上，求
的值．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
