
“點動成線,線動成面,面動成體”。如圖, 軸上有一條單位長度的線段
軸上有一條單位長度的線段 ,沿著與其垂直的
,沿著與其垂直的 軸方向平移一個單位長度,線段掃過的區域形成一個二維方體(正方形
軸方向平移一個單位長度,線段掃過的區域形成一個二維方體(正方形 ),再把正方形沿著與其所在的平面垂直的
),再把正方形沿著與其所在的平面垂直的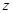 軸方向平移一個單位長度,則正方形掃過的區域形成一個三維方體(正方體
軸方向平移一個單位長度,則正方形掃過的區域形成一個三維方體(正方體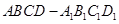 )。請你設想存在四維空間,將正方體向第四個維度平移得到四維方體,若一個四維方體有
)。請你設想存在四維空間,將正方體向第四個維度平移得到四維方體,若一個四維方體有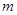 個頂點,
個頂點,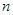 條棱,
條棱, 個面,則
個面,則 的值分別為 ( )
的值分別為 ( )
A. | B.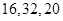 | C.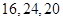 | D.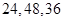 |
A
解析試題分析:依題意,線段AB平移到CD位置后,可形成正方形 ,它有四個頂點、四條棱(邊)、一個面;正方形
,它有四個頂點、四條棱(邊)、一個面;正方形 平移到正方形
平移到正方形 位置后,可形成正方體
位置后,可形成正方體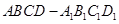 ,它有8個頂點、12條棱、6個面;
,它有8個頂點、12條棱、6個面;
把正方體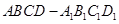 沿著與x軸、y軸、z軸都垂直的第四維方向進行平移得到四維方體后,
沿著與x軸、y軸、z軸都垂直的第四維方向進行平移得到四維方體后,
原來的8個頂點在平移后形成新的8個頂點,所以四維方體就共有8+8=16個頂點;
原先的8個頂點在平移的過程又形成新的8條棱,所以四維方體就共有12+12+8=32條棱;
正方體的12條棱在平移的過程都會形成一個新的面,所以四維方體就共有6+6+12=24個面;正方體的6個面在平移的過程中又各會形成一個正方體,所以四維方體中就包含有1+1+6=8個正方體.
考點:本小題主要考查類比推理.
點評:本題考查利用類比推理來說明空間中點線面之間的形成關系,解題的關鍵是理解點線面之間的:點動成線,線動成面,面動成體.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數學 來源: 題型:單選題
正四面體ABCD(六條棱長都相等)的棱長為1,棱AB∥平面,則正四面體上的所有點在平面 內的射影構成的圖形面積的取值范圍是( )
內的射影構成的圖形面積的取值范圍是( )
A.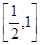 | B. | C.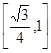 | D.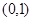 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
已知幾何體M的正視圖是一個面積為2 的半圓,俯視圖是正三角形,那么這個幾何體的表面積和體積為
的半圓,俯視圖是正三角形,那么這個幾何體的表面積和體積為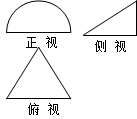
A.6 和 和  | B.6 +4 +4 和 和  |
C.6 +4 +4 和 和  | D.4( + + )和 )和  |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
球面上有三點A,B,C,其中OA,OB,OC兩兩互相垂直(O為球心),且過A、B、C三點的截面圓的面積為 ,則球的表面積( )
,則球的表面積( )
A、 B、
B、 C、
C、 D、
D、
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com