
【題目】已知圓C:(x+2)2+y2=1,P(x,y)為圓C上任一點(diǎn),
(1)求 ![]() 的最大、最小值;
的最大、最小值;
(2)求x﹣2y的最大、最小值.
【答案】
(1)解:設(shè)k= ![]() ,則y﹣2=kx﹣k,即直線方程為kx﹣y+2﹣k=0,
,則y﹣2=kx﹣k,即直線方程為kx﹣y+2﹣k=0,
∵P(x,y)為圓C上任一點(diǎn),
∴則圓心(﹣2,0)到直線的距離d= ![]() =
= ![]() ≤1,
≤1,
即|2﹣3k| ![]() ,
,
平方得8k2﹣12k+3≤0,
解得 ![]() ≤k≤
≤k≤ ![]() ,
,
故 ![]() 的最大值為
的最大值為 ![]() ,最小值為
,最小值為 ![]()
(2)解:設(shè)b=x﹣2y,j即x﹣2y﹣b=0,
∵P(x,y)為圓C上任一點(diǎn),
∴則圓心(﹣2,0)到直線的距離d= ![]() ,
,
即|b+2|≤ ![]() ,
,
則﹣2﹣ ![]() ≤b≤
≤b≤ ![]() ﹣2,
﹣2,
即x﹣2y的最大值為 ![]() ﹣2,最小值為﹣2﹣
﹣2,最小值為﹣2﹣ ![]()
【解析】(1)設(shè)k= ![]() ,利用直線和圓的位置關(guān)系即可得到結(jié)論;(2)設(shè)z=x﹣2y,利用直線和圓的位置關(guān)系即可得到結(jié)論.
,利用直線和圓的位置關(guān)系即可得到結(jié)論;(2)設(shè)z=x﹣2y,利用直線和圓的位置關(guān)系即可得到結(jié)論.
【考點(diǎn)精析】通過靈活運(yùn)用圓的標(biāo)準(zhǔn)方程,掌握圓的標(biāo)準(zhǔn)方程:![]() ;圓心為A(a,b),半徑為r的圓的方程即可以解答此題.
;圓心為A(a,b),半徑為r的圓的方程即可以解答此題.


 激活思維優(yōu)加課堂系列答案
激活思維優(yōu)加課堂系列答案 活力試卷系列答案
活力試卷系列答案 課課優(yōu)能力培優(yōu)100分系列答案
課課優(yōu)能力培優(yōu)100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了迎接珠海作為全國文明城市的復(fù)查,愛衛(wèi)會隨機(jī)抽取了60位路人進(jìn)行問卷調(diào)查,調(diào)查項(xiàng)目是自己對珠海各方面衛(wèi)生情況的滿意度(假設(shè)被問卷的路人回答是客觀的),以分?jǐn)?shù)表示問卷結(jié)果,并統(tǒng)計(jì)他們的問卷分?jǐn)?shù),把其中不低于50分的分成五段[50,60),[60,70),…[90,100]后畫出如圖部分頻率分布直方圖,觀察圖形信息,回答下列問題: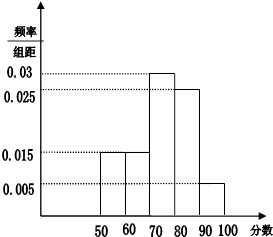
(1)求出問卷調(diào)查分?jǐn)?shù)低于50分的被問卷人數(shù);
(2)估計(jì)全市市民滿意度在60分及以上的百分比.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() 是拋物線
是拋物線![]() 的焦點(diǎn), 若點(diǎn)
的焦點(diǎn), 若點(diǎn)![]() 在
在![]() 上,且
上,且![]() .
.
(1)求![]() 的值;
的值;
(2)若直線![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() 且與
且與![]() 交于
交于![]() (異于
(異于![]() )兩點(diǎn), 證明: 直線
)兩點(diǎn), 證明: 直線![]() 與直線
與直線![]() 的斜率之積為常數(shù).
的斜率之積為常數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為備戰(zhàn)![]() 年瑞典乒乓球世界錦標(biāo)賽,乒乓球隊(duì)舉行公開選撥賽,甲、乙、丙三名選手入圍最終單打比賽名單.現(xiàn)甲、乙、丙三人進(jìn)行隊(duì)內(nèi)單打?qū)贡荣悾績扇吮荣愐粓觯操惾龍?/span>,每場比賽勝者得
年瑞典乒乓球世界錦標(biāo)賽,乒乓球隊(duì)舉行公開選撥賽,甲、乙、丙三名選手入圍最終單打比賽名單.現(xiàn)甲、乙、丙三人進(jìn)行隊(duì)內(nèi)單打?qū)贡荣悾績扇吮荣愐粓觯操惾龍?/span>,每場比賽勝者得![]() 分,負(fù)者得
分,負(fù)者得![]() 分,在每一場比賽中,甲勝乙的概率為
分,在每一場比賽中,甲勝乙的概率為![]() ,丙勝甲的概率為
,丙勝甲的概率為![]() ,乙勝丙的概率為
,乙勝丙的概率為![]() ,且各場比賽結(jié)果互不影響.若甲獲第一名且乙獲第三名的概率為
,且各場比賽結(jié)果互不影響.若甲獲第一名且乙獲第三名的概率為![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)設(shè)在該次對抗比賽中,丙得分為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,側(cè)面PAD⊥底面ABCD,側(cè)棱PA=PD= ![]() ,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn).
,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O為AD中點(diǎn). 
(1)求證:PO⊥平面ABCD;
(2)求異面直線PB與CD所成角的余弦值;
(3)線段AD上是否存在點(diǎn)Q,使得它到平面PCD的距離為 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com