
【題目】如圖,三棱柱ABC﹣A1B1C1中,側面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,
(Ⅰ)求證:AC⊥A1B;
(Ⅱ)求二面角A﹣A1C﹣B的余弦值.
【答案】(1) 見解析(2) ![]()
【解析】試題分析:(Ⅰ)作AC的中點O,由A1A=A1C,且O為AC的中點,得A1O⊥AC,再由面面垂直的性質可得A1O⊥底面ABC,以O為坐標原點,OB、OC、OA1所在直線分別為x、y、z軸建立空間直角坐標系,求出所用點的坐標,由![]() =0,可得AC⊥A1B;
=0,可得AC⊥A1B;
(Ⅱ)求出平面AA1C與平面A1CB的法向量,由兩法向量所成角的余弦值可得二面角A﹣A1C﹣B的余弦值.
試題解析:
(Ⅰ)證明:作AC的中點O,∵A1A=A1C,且O為AC的中點,∴A1O⊥AC,
又側面AA1C1C⊥底面ABC,其交線為AC,且A1O平面AA1C1C,
∴A1O⊥底面ABC,
以O為坐標原點,OB、OC、OA1所在直線分別為x、y、z軸建立空間直角坐標系,
由已知得:O(0,0,0),A(0,﹣1,0),A1(0,0,![]() ),C(0,1,0),C1(0,2,
),C(0,1,0),C1(0,2,![]() ),B(1,0,0).
),B(1,0,0).
則有:![]() ,
,![]() ,
,
∵![]() =0,∴AC⊥A1B;
=0,∴AC⊥A1B;
(Ⅱ)解:平面AA1C的一個法向量為![]() .
.
設平面A1CB的一個法向量![]() ,
,
由 ,取z=1,得
,取z=1,得![]() .
.
∴cos<![]() >=
>=![]() .
.
∴二面角A﹣A1C﹣B的余弦值為![]() .
.



科目:高中數學 來源: 題型:
【題目】某班同學利用國慶節進行社會實踐,對![]() 歲的人群隨機抽取
歲的人群隨機抽取![]() 人進行了一次生活習慣是否符合低碳觀念的調查,若生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得到如下統計表和各年齡段人數頻率分布直方圖:
人進行了一次生活習慣是否符合低碳觀念的調查,若生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得到如下統計表和各年齡段人數頻率分布直方圖:
組數 | 分組 | 低碳族的人數 | 占本組的頻率 |
第一組 |
| 120 | 0.6 |
第二組 |
| 195 |
|
第三組 |
| 100 | 0.5 |
第四組 |
|
| 0.4 |
第五組 |
| 30 | 0.3 |
第六組 |
| 15 | 0.3 |
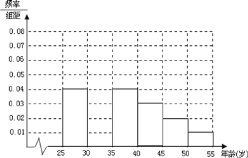
(1)補全頻率分布直方圖并求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)從![]() 歲年齡段的“低碳族”中采用分層抽樣法抽取18人參加戶外低碳體驗活動,如何抽取?
歲年齡段的“低碳族”中采用分層抽樣法抽取18人參加戶外低碳體驗活動,如何抽取?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠要建造一個長方形無蓋蓄水池,其容積為![]() 立方米,深為
立方米,深為![]() .如果池底每平方米的造價為
.如果池底每平方米的造價為![]() 元,池壁每平方米的造價為
元,池壁每平方米的造價為![]() 元,那么怎樣設計水池能使總造價最低(設蓄水池池底的相鄰兩邊邊長分別為
元,那么怎樣設計水池能使總造價最低(設蓄水池池底的相鄰兩邊邊長分別為![]() ,
,![]() )?最低總造價是多少?
)?最低總造價是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王在年初用50萬元購買一輛大貨車,第一年因繳納各種費用需支出6萬元,從第二年起,每年都比上一年增加支出2萬元,假定該車每年的運輸收入均為25萬元.小王在該車運輸累計收入超過總支出后,考慮將大貨車作為二手車出售,若該車在第x年年底出售,其銷售價格為25-x萬元(國家規定大貨車的報廢年限為10年).
(1)大貨車運輸到第幾年年底,該車運輸累計收入超過總支出?
(2)在第幾年年底將大貨車出售,能使小王獲得的年平均利潤最大(利潤=累計收入+銷售收入-總支出)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是正方形,側棱PD⊥底面ABCD,PD=DC,E是PC的中點,作EF⊥PB交PB于點F.

(Ⅰ)證明 PA//平面EDB;
(Ⅱ)證明PB⊥平面EFD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某年級教師年齡數據如下表:
年齡(歲) | 人數(人) |
22 | 1 |
28 | 2 |
29 | 3 |
30 | 5 |
31 | 4 |
32 | 3 |
40 | 2 |
合計 | 20 |
(1)求這20名教師年齡的眾數與極差;
(2)以十位數為莖,個位數為葉,作出這20名教師年齡的莖葉圖;
(3)現在要在年齡為29歲和31歲的教師中選2位教師參加學校有關會議,求所選的2位教師年齡不全相同的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com