【題目】已知函數
，給出下列結論:
（1）若對任意
，且
，都有
，則
為R上的減函數；
（2）若
為R上的偶函數，且在
內是減函數， 
（-2）=0，則
>0解集為（-2,2）；
（3）若
為R上的奇函數，則
也是R上的奇函數；
（4）t為常數，若對任意的
,都有
則
關于
對稱。
其中所有正確的結論序號為_________
科目：高中數學 來源： 題型：
【題目】已知如圖①，正三角形
的邊長為4，
是
邊上的高，
，
分別是
和
邊的中點，現將△
沿
翻折成直二面角
，如圖②．
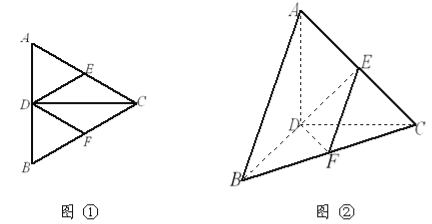
（1）判斷直線
與平面
的位置關系，并說明理由；
（2）求棱錐
的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,橢圓
(
)的離心率是
,過點
(
,
)的動直線
與橢圓相交于
,
兩點,當直線
平行于
軸時,直線
被橢圓
截得的線段長為
．
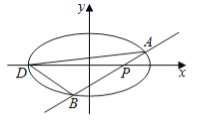
⑴求橢圓
的方程:
⑵已知
為橢圓的左端點,問: 是否存在直線
使得
的面積為
?若不存在,說明理由,若存在,求出直線
的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）甲、乙兩袋中各裝有大小相同的小球
個，其中甲袋中紅色、黑色、白色小球的個數分別為
、
、
，乙袋中紅色、黑色、白色小球的個數均為
，某人用左右手分別從甲、乙兩袋中取球．
（1）若左右手各取一球，求兩只手中所取的球顏色不同的概率；
（2）若左右手依次各取兩球，稱同一手中兩球顏色相同的取法為成功取法，記兩次取球的成功取法次數為隨機變量
，求
的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
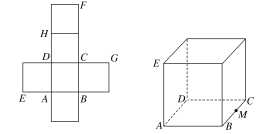
【題目】一個正方體的平面展開圖及該正方體直觀圖的示意圖如圖所示，在正方體中，設BC的中點為M，GH的中點為N。
(1)請將字母F，G，H標記在正方體相應的頂點處(不需說明理由)；
(2)證明：直線MN∥平面BDH；
(3)過點M，N，H的平面將正方體分割為兩部分，求這兩部分的體積比．
查看答案和解析>>
科目：高中數學 來源： 題型：
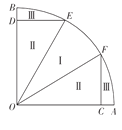
【題目】現有一個以
、
為半徑的扇形池塘，在
、
上分別取點
、
，作
、
分別交弧
于點
、
，且
，現用漁網沿著
、
、
、
將池塘分成如圖所示的養殖區域.已知
， 
， 
（
）.
（1）若區域Ⅱ的總面積為
，求
的值；
（2）若養殖區域Ⅰ、Ⅱ、Ⅲ的每平方千米的年收入分別是30萬元、40萬元、20萬元，試問：當
為多少時，年總收入最大？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
