
【題目】設二次函數![]() 滿足下列條件:
滿足下列條件:
①![]() 對
對![]() 恒成立; ②
恒成立; ②![]() 對
對![]() 恒成立.
恒成立.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的解析式;
的解析式;
(3)求最大的實數![]() ,使得存在實數
,使得存在實數![]() ,當
,當![]() 時,
時, ![]() 恒成立.
恒成立.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】試題分析:(1)由當x∈(0,5)時,都有x≤f(x)≤2|x﹣1|+1恒成立可得f(1)=1;
(2)由f(﹣1+x)=f(﹣1﹣x)可得二次函數f(x)=ax2+bx+c(a,b,c∈R)的對稱軸為x=﹣1,于是b=2a,再由f(x)min=f(﹣1)=0,可得c=a,從而可求得函數f(x)的解析式;
(3)可由f(1+t)≤1,求得:﹣4≤t≤0,再利用平移的知識求得最大的實數m.
試題解析:
(1)當x=1時, ![]()
(2)由已知可得![]() ……①
……①
由![]() ……②
……②
![]()
由![]() 恒成立
恒成立![]() 對R恒成立
對R恒成立
則![]()
![]()
由![]() 對
對![]() 恒成立
恒成立
![]() 恒成立
恒成立
則![]()

![]() ,
,![]()
(3)![]() 恒成立,則使
恒成立,則使![]() 的圖像在
的圖像在![]() 的下方,且m最大,則1,m為
的下方,且m最大,則1,m為![]() 的兩個根
的兩個根
由![]()
![]()
![]()
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)是奇函數,且滿足f(x)=f(x+3),f(-2)=-3.若數列{an}中,a1=-1,且前n項和Sn滿足![]() =2×
=2×![]() +1,則f(a5)+f(a6)=________.
+1,則f(a5)+f(a6)=________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,給出下列結論:
,給出下列結論:
(1)若對任意![]() ,且
,且![]() ,都有
,都有![]() ,則
,則![]() 為R上的減函數;
為R上的減函數;
(2)若![]() 為R上的偶函數,且在
為R上的偶函數,且在![]() 內是減函數,
內是減函數, ![]() (-2)=0,則
(-2)=0,則![]() >0解集為(-2,2);
>0解集為(-2,2);
(3)若![]() 為R上的奇函數,則
為R上的奇函數,則![]() 也是R上的奇函數;
也是R上的奇函數;
(4)t為常數,若對任意的![]() ,都有
,都有![]() 則
則![]() 關于
關于![]() 對稱。
對稱。
其中所有正確的結論序號為_________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知直線![]() 的參數方程為
的參數方程為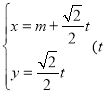 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .且曲線
.且曲線![]() 的左焦點
的左焦點![]() 在直線
在直線![]() 上.
上.
(1)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值;
的值;
(2)求曲線![]() 的內接矩形的周長的最大值.
的內接矩形的周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ;
;
(1)若f(x)的定義域為 (-∞,+∞), 求實數a的范圍;
(2)若f(x)的值域為 [0, +∞), 求實數a的范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P(2,2),圓C:x2+y2-8y=0,過點P的動直線l與圓C交于A,B兩點,線段AB的中點為M,O為坐標原點.
(1)求M的軌跡方程;
(2)當|OP|=|OM|時,求l的方程及△POM的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過曲線C1:![]() -
-![]() =1(a>0,b>0)的左焦點F1作曲線C2:x2+y2=a2的切線,設切點為M,直線F1M交曲線C3:y2=2px(p>0)于點N,其中曲線C1與C3有一個共同的焦點,若|MF1|=|MN|,則曲線C1的離心率為( )
=1(a>0,b>0)的左焦點F1作曲線C2:x2+y2=a2的切線,設切點為M,直線F1M交曲線C3:y2=2px(p>0)于點N,其中曲線C1與C3有一個共同的焦點,若|MF1|=|MN|,則曲線C1的離心率為( )
A. ![]() B.
B. ![]() -1 C.
-1 C. ![]() +1 D.
+1 D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】化為推出一款6寸大屏手機,現對500名該手機使用者(200名女性,300名男性)進行調查,對手機進行打分,打分的頻數分布表如下:
女性用戶:
分值區間 |
|
|
|
|
|
頻數 | 20 | 40 | 80 | 50 | 10 |
分值區間 |
|
|
|
|
|
頻數 | 45 | 75 | 90 | 60 | 30 |
男性用戶:
(1)如果評分不低于70分,就表示該用戶對手機“認可”,否則就表示“不認可”,完成下列![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為性別對手機的“認可”有關:
的把握認為性別對手機的“認可”有關:
女性用戶 | 男性用戶 | 合計 | |
“認可”手機 | |||
“不認可”手機 | |||
合計 |
附:
| 0.05 | 0.01 |
| 3.841 | 6635 |
![]()
(2)根據評分的不同,運用分層抽樣從男性用戶中抽取20名用戶,在這20名用戶中,從評分不低于80分的用戶中任意抽取3名用戶,求3名用戶中評分小于90分的人數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln x+![]() +ax(a是實數),g(x)=
+ax(a是實數),g(x)=![]() +1.
+1.
(1)當a=2時,求函數f(x)在定義域上的最值;
(2)若函數f(x)在[1,+∞)上是單調函數,求a的取值范圍;
(3)是否存在正實數a滿足:對于任意x1∈[1,2],總存在x2∈[1,2],使得f(x1)=g(x2)成立? 若存在,求出a的取值范圍,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com