【題目】已知函數
（1）討論的單調性
；
（2）若
有兩個零點，求
的取值范圍.
【答案】(1) 
在
上遞減，在
上遞增(2) 
【解析】試題分析：（1）求出
，分類討論，分別由
可得增區間，由
可得減區間；（2）由（1）可知，當
時才有兩個零點，根據函數的單調性求得
最小值，由
，求導，由
，即可求得
的取值范圍.
試題解析：（1）由
，當
時， 
， 
當
單調遞減，當
時， 
，當
單調遞增，當
時， 
單調遞減，當
時， 
恒成立， 
當
單調遞減，綜上可知，當
時， 
在
上單調減函數，當
時， 
在
是減函數，在
是增函數.
（2）若
時，由（1）可知， 
最多有一個零點，當
時， 
，當
時， 
， 
當
時， 
，當
，且遠遠大于
和
， 
當
， 
函數有兩個零點， 
的最小值小于
即可，由
在
是減函數，在
是增函數， 
，
，即
，設
，則
，求導
，由
，解得
， 
的取值范圍
.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】圓O1和圓O2的極坐標方程分別為ρ＝4cosθ，ρ＝－4sinθ
（1）把圓O1和圓O2的極坐標方程化為直角坐標方程；
（2）求經過圓O1、圓O2交點的直線的直角坐標方程
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數y=f（x）的定義域是[0，4]，則函數g（x）= 
的定義域是（ ）
A.[0，2]
B.[0，2）
C.[0，1）∪（1，2]
D.[0，4]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，A ， B ， C是三個觀察站，A在B的正東，兩地相距6km，C在B的北偏西30°，兩地相距4km，在某一時刻，A觀察站發現某種信號，并知道該信號的傳播速度為1km/s,4s后B ， C兩個觀察站同時發現這種信號，在以過A ， B兩點的直線為x軸，以AB的垂直平分線為y軸建立的平面直角坐標系中，指出發出這種信號的P的坐標．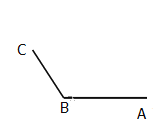
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為考察高中生的性別與喜歡數學課程之間的關系，在某學校高中生中隨機抽取了250名學生，得到如圖的二維條形圖.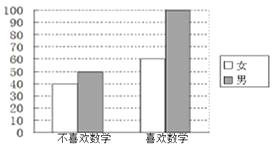
（1）根據二維條形圖，完成下表：
男 | 女 | 合計 | |
喜歡數學課程 | |||
不喜歡數學課程 | |||
合計 |
（2）對照如表，利用列聯表的獨立性檢驗估計，請問有多大把握認為“性別與喜歡數學有關系”？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xoy中，直線l的參數方程為
（t為參數）．在以原點O為極點，x軸正半軸為極軸的極坐標系中，圓C的方程為ρ=4cosθ．
（1）寫出直線l的普通方程和圓C的直角坐標方程．
（2）若點P坐標為（1，1），圓C與直線l交于A，B兩點，求|PA|+|PB|的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一列火車從重慶駛往北京，沿途有n個車站（包括起點站重慶和終點站北京）．車上有一郵政車廂，每停靠一站便要卸下火車已經過的各站發往該站的郵袋各1個，同時又要裝上該站發往以后各站的郵袋各1個，設從第k站出發時，郵政車廂內共有郵袋ak個（k=1，2，…，n）．
（1）求數列{ak}的通項公式；
（2）當k為何值時，ak的值最大，求出ak的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
