
【題目】已知曲線![]() 上的點到點
上的點到點![]() 的距離比它到直線
的距離比它到直線![]() 的距離小2.
的距離小2.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() ,
, ![]() 兩點,若
兩點,若![]() ,當
,當![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)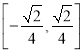
【解析】試題分析:(1)由題意得曲線![]() 是以
是以![]() 為焦點,以
為焦點,以![]() 為準線的拋物線,進而可得其方程為
為準線的拋物線,進而可得其方程為![]() ;(2)設直線
;(2)設直線![]() 為
為![]() ,代入拋物線方程消去
,代入拋物線方程消去![]() 可得
可得![]() ,設
,設![]() ,
, ![]() ,則
,則![]() ,由
,由![]() ,得
,得![]() ,又
,又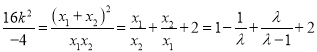 ,可構造
,可構造![]() ,由函數(shù)的單調性可得
,由函數(shù)的單調性可得![]() ,即
,即![]() ,解得
,解得![]() ,即為所求。
,即為所求。
試題解析:(1)由題意得動點![]() 到
到![]() 的距離等于它到直線
的距離等于它到直線![]() 的距離,
的距離,
∴ 動點![]() 的軌跡是以
的軌跡是以![]() 為焦點,以
為焦點,以![]() 為準線的拋物線,
為準線的拋物線,
設其方程為![]() ,由條件得
,由條件得![]() .
.
∴ 曲線![]() 的標準方程為
的標準方程為![]() ;
;
(2)由題意設直線![]() 的方程為
的方程為![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
∵ 直線![]() 與拋物線相交,∴
與拋物線相交,∴![]() ,
,
設A(x1,y1),B(x2,y2),則![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
由![]() 可得
可得
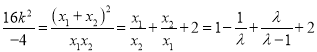 ,
,
即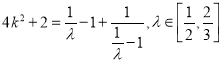 ,
,
∵![]() ,∴
,∴![]() 。
。
設![]() ,則函數(shù)
,則函數(shù)![]() 在
在![]() 上單調遞減。
上單調遞減。
∴![]() ,即
,即![]() 。
。
由![]() 得
得![]() ,滿足
,滿足![]() 。
。
∴![]() 的取值范圍為
的取值范圍為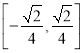 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
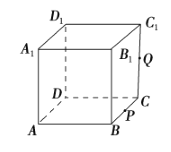
【題目】如圖,正方體![]() 的棱長為 1,
的棱長為 1, ![]() 為
為![]() 的中點,
的中點, ![]() 為線段
為線段![]() 上的動點,過點A、P、Q的平面截該正方體所得的截面記為
上的動點,過點A、P、Q的平面截該正方體所得的截面記為![]() .則下列命題正確的是__________(寫出所有正確命題的編號).
.則下列命題正確的是__________(寫出所有正確命題的編號).
①當![]() 時,
時, ![]() 為四邊形;②當
為四邊形;②當![]() 時,
時, ![]() 為等腰梯形;③當
為等腰梯形;③當![]() 時,
時, ![]() 為六邊形;④當
為六邊形;④當![]() 時,
時, ![]() 的面積為
的面積為![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點M是圓心為E的圓![]() 上的動點,點
上的動點,點![]() ,線段MF的垂直平分線交EM于點P.
,線段MF的垂直平分線交EM于點P.
(Ⅰ)求動點P的軌跡C的方程;
(Ⅱ)過原點O作直線交(Ⅰ)中軌跡C于點A、B,點D滿足![]() ,試求四邊形AFBD的面積的取值范圍.
,試求四邊形AFBD的面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在三棱錐D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E為BC的中點,F在棱AC上,且AF=3FC
(1)求三棱錐D-ABC的體積
(2)求證:平面DAC⊥平面DEF;
(3)若M為DB中點,N在棱AC上,且CN=![]() CA,求證:MN∥平面DEF
CA,求證:MN∥平面DEF

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在各項均為正數(shù)的等比數(shù)列![]() 中,
中, ![]() ,且
,且![]() 成等差數(shù)列.
成等差數(shù)列.
(1)求等比數(shù)列![]() 的通項公式;
的通項公式;
(2)若數(shù)列![]() 滿足
滿足![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項和
項和![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知坐標平面上點![]() 與兩個定點
與兩個定點![]() ,
, ![]() 的距離之比等于5.
的距離之比等于5.
(1)求點![]() 的軌跡方程,并說明軌跡是什么圖形;
的軌跡方程,并說明軌跡是什么圖形;
(2)記(1)中的軌跡為![]() ,過點
,過點![]() 的直線
的直線![]() 被
被![]() 所截得的線段的長為8,求直線
所截得的線段的長為8,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)= ![]()
(1)若對![]() ,f(x)
,f(x) ![]() 恒成立,求的取值范圍;
恒成立,求的取值范圍;
(2)已知常數(shù)a![]() R,解關于x的不等式f(x)
R,解關于x的不等式f(x) ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】從某居民區(qū)隨機抽取10個家庭,獲得第i個家庭的月收入xi(單位:千元)與月儲蓄yi(單位:千元)的數(shù)據(jù)資料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月儲蓄y對月收入x的線性回歸方程y=bx+a;
(2)判斷變量x與y之間是正相關還是負相關;
(3)若該居民區(qū)某家庭月收入為7千元,預測該家庭的月儲蓄.
附:線性回歸方程y=bx+a中,  ,a=
,a=![]() -b
-b![]() ,其中
,其中![]() ,
, ![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com