
【題目】已知![]() ,
, ![]() 是拋物線
是拋物線![]() 上兩點,且
上兩點,且![]() 與
與![]() 兩點橫坐標之和為3.
兩點橫坐標之和為3.
(1)求直線![]() 的斜率;
的斜率;
(2)若直線![]() ,直線
,直線![]() 與拋物線相切于點
與拋物線相切于點![]() ,且
,且![]() ,求
,求![]() 方程.
方程.
【答案】(1)直線![]() 的斜率為
的斜率為![]() ;(2)
;(2)![]() 方程為
方程為![]() .
.
【解析】試題分析:(1)根據已知條件,設直線AB的解析式為y=kx+t,聯立直線和拋物線的解析式,利用A與B的橫坐標之和為3,結合一元二次方程的根與系數的關系求出k的值;
(2)設出過點M的切線方程![]() ,由切線與曲線只有一個交點,確定點M的坐標;再利用AM⊥BM可得kAM·kBM=-1,將相應的值代入,再結合根與系數的關系進行計算,求出b即可得到答案.
,由切線與曲線只有一個交點,確定點M的坐標;再利用AM⊥BM可得kAM·kBM=-1,將相應的值代入,再結合根與系數的關系進行計算,求出b即可得到答案.
試題解析:(1)設![]() 方程為
方程為![]() ,則由
,則由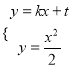 ,得
,得![]() ,
,
![]() 時,設
時,設![]() ,
, ![]() ,則
,則![]() ,
,
又![]() ,∴
,∴![]() ,即直線
,即直線![]() 的斜率為
的斜率為![]() .
.
(2)∵![]() ,∴可設
,∴可設![]() 方程為
方程為![]() ,∴
,∴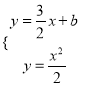 ,得
,得![]() ,
,
∵![]() 是切線,∴
是切線,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
, ![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
又![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() 或
或![]() ,
,
又![]() ,∴
,∴![]() 方程為
方程為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,直線
,直線![]() 過拋物線焦點,且與拋物線交于
過拋物線焦點,且與拋物線交于![]() ,
, ![]() 兩點,以線段
兩點,以線段![]() 為直徑的圓與拋物線準線的位置關系是( )
為直徑的圓與拋物線準線的位置關系是( )
A. 相離 B. 相交 C. 相切 D. 不確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() 是棱PD的中點,且
是棱PD的中點,且![]() ,
, ![]() .
.
(I)求證: ![]() ; (Ⅱ)求二面角
; (Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() 是
是![]() 上一點,且直線
上一點,且直線![]() 與平面
與平面![]() 成角的正弦值為
成角的正弦值為![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年9月3日,抗戰勝利71周年紀念活動在北京隆重舉行,受到全國人民的矚目.紀念活動包括舉行紀念大會、閱兵式、擁待會和文藝晚會等,據統計,抗戰老兵由于身體原因,參加紀念大會、閱兵式、招待會這個環節(可參加多個,也可都不參加)的情況及其概率如下表所示:

(Ⅰ)若m=2n,則從這60名抗戰老兵中按照參加紀念活動的環節數分層抽取6人進行座談,求從參加紀念活動環節數為1的抗戰老兵中抽取的人數;
(Ⅱ)某醫療部門決定從(Ⅰ)中抽取的6名抗戰老兵中隨機抽取2名進行體檢,求這2名抗戰老兵中至少有1人參加紀念活動的環節數為3的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓x2+![]() =1(0<b<1)的左焦點為F,左、右頂點分別為A、C,上頂點為B,過F、B、C三點作圓P,其中圓心P的坐標為(m,n).
=1(0<b<1)的左焦點為F,左、右頂點分別為A、C,上頂點為B,過F、B、C三點作圓P,其中圓心P的坐標為(m,n).
(1)若FC是圓P的直徑,求橢圓的離心率;
(2)若圓P的圓心在直線x+y=0上,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
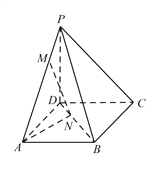
【題目】如圖,四棱錐 ![]() 底面為正方形,已知
底面為正方形,已知 ![]() ,
,![]() ,點
,點 ![]() 為線段
為線段 ![]() 上任意一點(不含端點),點
上任意一點(不含端點),點 ![]() 在線段
在線段 ![]() 上,且
上,且 ![]() .
.
(1)求證:![]() ;
;
(2)若 ![]() 為線段
為線段 ![]() 中點,求直線
中點,求直線 ![]() 與平面
與平面 ![]() 所成的角的余弦值.
所成的角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是異面直線,給出下列結論:
是異面直線,給出下列結論:
①一定存在平面![]() ,使直線
,使直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ;
;
②一定存在平面![]() ,使直線
,使直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ;
;
③一定存在無數個平面![]() ,使直線
,使直線![]() 與平面
與平面![]() 交于一個定點,且直線
交于一個定點,且直線![]() 平面
平面![]() .
.
則所有正確結論的序號為( )
A. ①② B. ② C. ②③ D. ③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com