
【題目】已知四棱錐![]() ,四邊形
,四邊形![]() 是正方形,
是正方形, ![]() .
.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 的中點,求二面角
的中點,求二面角![]() 的余弦值.
的余弦值.

【答案】(1)見解析(2) ![]()
【解析】試題分析:(1)由![]() 可得
可得![]() ,即
,即![]() ,由
,由![]() 為正方形,可得
為正方形,可得![]() ,從而得
,從而得![]() 平面
平面![]() ,由面面垂直的判定定理可得平面
,由面面垂直的判定定理可得平面![]() 平面
平面![]() ;(2)設
;(2)設![]() 的中點為
的中點為![]() ,∵
,∵![]() ,∴
,∴![]() ,面面垂直的性質(zhì)可得
,面面垂直的性質(zhì)可得![]() 平面
平面![]() ,在平面
,在平面![]() 內(nèi),過
內(nèi),過![]() 作直線
作直線![]() ,則
,則![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,
為坐標原點, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸,建立空間直角坐標系,分別根據(jù)向量垂直數(shù)量積為零列方程組求出平面
軸,建立空間直角坐標系,分別根據(jù)向量垂直數(shù)量積為零列方程組求出平面![]() 與平面
與平面![]() 的一個法向量,根據(jù)空間向量夾角余弦公式,可得結果.
的一個法向量,根據(jù)空間向量夾角余弦公式,可得結果.
試題解析:(1)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() 為正方形,∴
為正方形,∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)
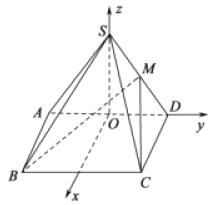
設![]() 的中點為
的中點為![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
由(1)可知平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
在平面![]() 內(nèi),過
內(nèi),過![]() 作直線
作直線![]() ,則
,則![]() 兩兩垂直.
兩兩垂直.
以![]() 為坐標原點,
為坐標原點, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,
則 ,
,
∴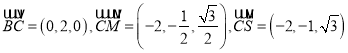 ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,
, 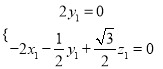 ,即
,即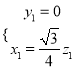 ,取
,取![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() ,
, 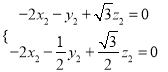 ,即
,即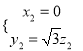 ,取
,取![]() ,
,
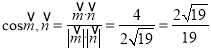 ,由圖可知,二面角
,由圖可知,二面角![]() 的余弦值為
的余弦值為![]() .
.
【方法點晴】本題主要考查面面垂直的判定定理以及利用空間向量求二面角,屬于難題.空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當?shù)目臻g直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數(shù)量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據(jù)定理結論求出相應的角和距離.


科目:高中數(shù)學 來源: 題型:
【題目】下列函數(shù)中與f(x)=x是同一函數(shù)的有( )
①y=![]() ②y=
②y=![]() ③y=
③y=![]() ④y=
④y=![]() ⑤f(t)=t⑥g(x)=x
⑤f(t)=t⑥g(x)=x
A. 1 個 B. 2 個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知f(xy)=f(x)+f(y).
(1) 若x,y∈R,求f(1),f(-1)的值; (2)若x,y∈R,判斷y=f(x)的奇偶性;
(3)若函數(shù)f(x)在其定義域(0,+∞)上是增函數(shù),f(2)=1,f(x)+f(x-2)≤3,求x的取值范圍。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市“招手即停”公共汽車的票價按下列規(guī)則制定:
5公里以內(nèi)(含5公里),票價2元;
5公里以上,每增加5公里,票價增加1元(不足5公里的按5公里計算).如果某條線路的總里程為20公里,請根據(jù)題意.
(1)寫出票價與里程之間的函數(shù)解析式;
(2)根據(jù)(1)寫出的函數(shù)解析式試畫出該函數(shù)的圖象.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】兩個隨機變量x,y的取值表為
x | 0 | 1 | 3 | 4 |
y | 2.2 | 4.3 | 4.8 | 6.7 |
若x,y具有線性相關關系,且 ![]() =
= ![]() x+2.6,則下列四個結論錯誤的是( )
x+2.6,則下列四個結論錯誤的是( )
A.x與y是正相關
B.當x=6時,y的估計值為8.3
C.x每增加一個單位,y增加0.95個單位
D.樣本點(3,4.8)的殘差為0.56
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱豬ABCD﹣A1B1C1D1中,側棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,A1A=AB=2,E為棱AA1的中點.
(1)證明:B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點![]() 與點
與點![]() 的距離比它的直線
的距離比它的直線![]() 的距離小2.
的距離小2.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)![]() 是點
是點![]() 軌跡上互相垂直的兩條弦,問:直線
軌跡上互相垂直的兩條弦,問:直線![]() 是否經(jīng)過
是否經(jīng)過![]() 軸上一定點,若經(jīng)過,求出該點坐標;若不經(jīng)過,說明理由.
軸上一定點,若經(jīng)過,求出該點坐標;若不經(jīng)過,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的定義域為
的定義域為![]() ,若
,若![]() 在
在![]() 上為增函數(shù),則稱
上為增函數(shù),則稱![]() 為“一階比增函數(shù)”.
為“一階比增函數(shù)”.
(1)若![]() 是“一階比增函數(shù)”,求實數(shù)a的取值范圍。
是“一階比增函數(shù)”,求實數(shù)a的取值范圍。
(2)若![]() 是“一階比增函數(shù)”,求證:對任意
是“一階比增函數(shù)”,求證:對任意![]() ,
,![]() ,總有
,總有![]() ;
;
(3)若![]() 是“一階比增函數(shù)”,且
是“一階比增函數(shù)”,且![]() 有零點,求證:關于x的不等式
有零點,求證:關于x的不等式![]() 有解.
有解.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的上下兩個焦點分別為
的上下兩個焦點分別為![]() ,
, ![]() ,過點
,過點![]() 與
與![]() 軸垂直的直線交橢圓
軸垂直的直線交橢圓![]() 于
于![]() 、
、![]() 兩點,
兩點, ![]() 的面積為
的面積為![]() ,橢圓
,橢圓![]() 的離心力為
的離心力為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)已知![]() 為坐標原點,直線
為坐標原點,直線![]() :
: ![]() 與
與![]() 軸交于點
軸交于點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
, ![]() 兩個不同的點,若存在實數(shù)
兩個不同的點,若存在實數(shù)![]() ,使得
,使得![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com