
【題目】設數列![]() 的前n項和為
的前n項和為![]() ,
,![]()
(1)求證:數列![]() 是等比數列;
是等比數列;
(2)若![]() ,是否存在q的某些取值,使數列
,是否存在q的某些取值,使數列![]() 中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
中某一項能表示為另外三項之和?若能求出q的全部取值集合,若不能說明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使數列
,使數列![]() 中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
中,某一項可以表示為另外三項之和?若存在指出q的一個取值,若不存在,說明理由.
科目:高中數學 來源: 題型:
【題目】如圖,已知直線![]() 交拋物線
交拋物線![]() 于
于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側),過線段
左側),過線段![]() (兩端點除外)上的任意一點作直線
(兩端點除外)上的任意一點作直線![]() ,使得直線
,使得直線![]() 與拋物線
與拋物線![]() 在點
在點![]() 處的切線平行,設直線
處的切線平行,設直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 、
、![]() 兩點.
兩點.
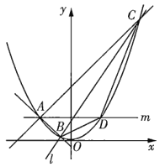
(1)記直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,證明:
,證明:![]() ;
;
(2)若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正四棱錐![]() 中,
中,![]() 是邊長為3的等邊三角形,點M是
是邊長為3的等邊三角形,點M是![]() 的重心,過點M作與平面PAC垂直的平面
的重心,過點M作與平面PAC垂直的平面![]() ,平面
,平面![]() 與截面PAC交線段的長度為2,則平面
與截面PAC交線段的長度為2,則平面![]() 與正四棱椎
與正四棱椎![]() 表面交線所圍成的封閉圖形的面積可能為______________.(請將可能的結果序號填到橫線上)①2;②
表面交線所圍成的封閉圖形的面積可能為______________.(請將可能的結果序號填到橫線上)①2;②![]() ;③3; ④
;③3; ④![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=2sinx(sinx![]() cosx)﹣1圖象向右平移
cosx)﹣1圖象向右平移![]() 個單位得函數g(x)的圖象,則下列命題中正確的是( )
個單位得函數g(x)的圖象,則下列命題中正確的是( )
A.f(x)在(![]() ,
,![]() )上單調遞增
)上單調遞增
B.函數f(x)的圖象關于直線x![]() 對稱
對稱
C.g(x)=2cos2x
D.函數g(x)的圖象關于點(![]() ,0)對稱
,0)對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】很多關于整數規律的猜想都通俗易懂,吸引了大量的數學家和數學愛好者,有些猜想已經被數學家證明,如“費馬大定理”,但大多猜想還未被證明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的內容是:對于每一個正整數,如果它是奇數,則將它乘以![]() 再加1;如果它是偶數,則將它除以
再加1;如果它是偶數,則將它除以![]() ;如此循環,最終都能夠得到
;如此循環,最終都能夠得到![]() .下圖為研究“角谷猜想”的一個程序框圖.若輸入
.下圖為研究“角谷猜想”的一個程序框圖.若輸入![]() 的值為
的值為![]() ,則輸出i的值為( )
,則輸出i的值為( )
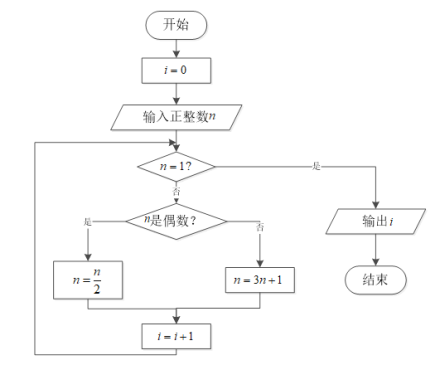
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com