
【題目】某小區為了加強對“新型冠狀病毒”的防控,確保居民在小區封閉期間生活不受影響,小區超市采取有力措施保障居民正常生活物資供應.為做好甲類生活物資的供應,超市對社區居民戶每天對甲類生活物資的購買量進行了調查,得到了以下頻率分布直方圖.
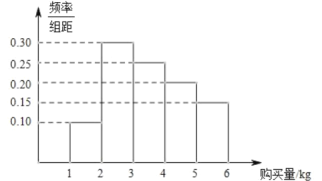
(1)從小區超市某天購買甲類生活物資的居民戶中任意選取5戶.
①若將頻率視為概率,求至少有兩戶購買量在![]() (單位:
(單位:![]() )的概率是多少?
)的概率是多少?
②若抽取的5戶中購買量在![]() (單位:
(單位:![]() )的戶數為2戶,從5戶中選出3戶進行生活情況調查,記3戶中需求量在
)的戶數為2戶,從5戶中選出3戶進行生活情況調查,記3戶中需求量在![]() (單位:
(單位:![]() )的戶數為
)的戶數為![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(2)將某戶某天購買甲類生活物資的量與平均購買量比較,當超出平均購買量不少于![]() 時,則稱該居民戶稱為“迫切需求戶”,若從小區隨機抽取10戶,且抽到k戶為“迫切需求戶”的可能性最大,試求k的值.
時,則稱該居民戶稱為“迫切需求戶”,若從小區隨機抽取10戶,且抽到k戶為“迫切需求戶”的可能性最大,試求k的值.
【答案】(1)①![]() ;②詳見解析;(2)
;②詳見解析;(2)![]() .
.
【解析】
(1)事件“從小區超市購買甲類物資的居民戶中任意選取1戶,購買量在![]() ,
,![]() ”發生的概率為
”發生的概率為![]() .
.
①記事件“從小區超市購買甲類物資的居民戶中任意選取5戶,則至少有兩戶購買量在![]() ,
,![]() ”為
”為![]() ,利用獨立重復實驗的概率求解即可.
,利用獨立重復實驗的概率求解即可.
②隨機變量![]() 所有可能的取值為0,1,2.求出概率得到分布列,然后求解期望.
所有可能的取值為0,1,2.求出概率得到分布列,然后求解期望.
(2)每天對甲類物資的購買量平均值,求出從小區隨機抽取中隨機抽取一戶為“迫切需求戶”的概率為![]() ,判斷
,判斷![]() ,通過若
,通過若![]() 戶的可能性最大,列出不等式組,求解
戶的可能性最大,列出不等式組,求解![]() 即可.
即可.
(1)由題意,事件“從小區超市購買甲類生活物資的居民戶中任意選取1戶,購買量在![]() ”發生的概率為
”發生的概率為![]() .
.
①記事件“從小區超市購買甲類生活物資的居民戶中任意選取5戶,則至少有兩戶購買量在![]() ”為A,則
”為A,則![]() .
.
②隨機變量![]() 所有可能的取值為0,1,2.則
所有可能的取值為0,1,2.則
![]() ,
,![]() ,
,![]() ,
,
| 0 | 1 | 2 |
|
|
|
|
所以![]()
(2)每天對甲類生活物資的需求平均值為
![]() (
(![]() )
)
則購買甲類生活物資為“迫切需求戶”的購買量為![]() ,從小區隨機抽取中隨機抽取一戶為“迫切需求戶”的概率為
,從小區隨機抽取中隨機抽取一戶為“迫切需求戶”的概率為![]() ,
,
若從小區隨機抽取10戶,且抽到X戶為“迫切需求戶”,![]() ,
,
若k戶的可能性最大,則![]() ,
,![]()
 ,得
,得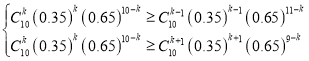 ,
,
解得![]() ,由于
,由于![]() ,故
,故![]() .
.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源: 題型:
【題目】近年來,國家相關政策大力鼓勵創新創業種植業戶小李便是受益者之一,自從2017年畢業以來,其通過自主創業而種植的某種農產品廣受市場青睞,他的種植基地也相應地新增加了一個平時小李便帶著部分員工往返于新舊基地之間進行科學管理和經驗交流,新舊基地之間開車單程所需時間為![]() ,由于不同時間段車流量的影響,現對50名員工往返新舊基地之間的用時情況進行統計,結果如下:
,由于不同時間段車流量的影響,現對50名員工往返新舊基地之間的用時情況進行統計,結果如下:
| 30 | 35 | 40 | 45 | 50 |
頻數(人) | 10 | 20 | 10 | 5 | 5 |
(1)若有50名員工參與調查,現從單程時間在35分鐘,40分鐘,45分鐘的人員中按分層抽樣的方法抽取7人,再從這7人中隨機抽取3人進行座談,用![]() 表示抽取的3人中時間在40分鐘的人數,求
表示抽取的3人中時間在40分鐘的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)某天,小李需要從舊基地駕車趕往新基地召開一個20分鐘的緊急會議,結束后立即返回舊基地.(以50名員工往返新舊基地之間的用時的頻率作為用時發生的概率)
①求小李從離開舊基地到返回舊基地共用時間不超過110分鐘的概率;
②若用隨機抽樣的方法從舊基地抽取8名骨干員工陪同小李前往新基地參加此次會議,其中有![]() 名員工從離開舊基地到返回舊基地共用時間不超過110分鐘,求隨機變量
名員工從離開舊基地到返回舊基地共用時間不超過110分鐘,求隨機變量![]() 的方差.
的方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() ,
,![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程
的極坐標方程![]() .
.
(1)若曲線![]() 與
與![]() 只有一個公共點,求
只有一個公共點,求![]() 的值;
的值;
(2)![]() 為曲線
為曲線![]() 上的兩點,且
上的兩點,且![]() ,求
,求![]() 的面積最大值.
的面積最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)若![]() .
.
①設![]() ,求證:數列
,求證:數列![]() 是等比數列;
是等比數列;
②若數列![]() 的前
的前![]() 項和
項和![]() 滿足
滿足![]() ,求實數
,求實數![]() 的最小值;
的最小值;
(2)若數列![]() 的奇數項與偶數項分別成等差數列,且
的奇數項與偶數項分別成等差數列,且![]() ,
,![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為實現有效利用扶貧資金,增加貧困村民的收入,扶貧工作組結合某貧困村水質優良的特點,決定利用扶貧資金從外地購買甲、乙、丙三種魚苗在魚塘中進行養殖試驗,試驗后選擇其中一種進行大面積養殖,已知魚苗甲的自然成活率為0.8.魚苗乙,丙的自然成活率均為0.9,且甲、乙、丙三種魚苗是否成活相互獨立.
(1)試驗時從甲、乙,丙三種魚苗中各取一尾,記自然成活的尾數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)試驗后發現乙種魚苗較好,扶貧工作組決定購買![]() 尾乙種魚苗進行大面積養殖,為提高魚苗的成活率,工作組采取增氧措施,該措施實施對能夠自然成活的魚苗不產生影響.使不能自然成活的魚苗的成活率提高了50%.若每尾乙種魚苗最終成活后可獲利10元,不成活則虧損2元,且扶貧工作組的扶貧目標是獲利不低于37.6萬元,問需至少購買多少尾乙種魚苗?
尾乙種魚苗進行大面積養殖,為提高魚苗的成活率,工作組采取增氧措施,該措施實施對能夠自然成活的魚苗不產生影響.使不能自然成活的魚苗的成活率提高了50%.若每尾乙種魚苗最終成活后可獲利10元,不成活則虧損2元,且扶貧工作組的扶貧目標是獲利不低于37.6萬元,問需至少購買多少尾乙種魚苗?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應“文化強國建設”號召,并增加學生們對古典文學的學習興趣,雅禮中學計劃建設一個古典文學熏陶室.為了解學生閱讀需求,隨機抽取200名學生做統計調查.統計顯示,男生喜歡閱讀古典文學的有64人,不喜歡的有56人;女生喜歡閱讀古典文學的有36人,不喜歡的有44人.
(1)能否在犯錯誤的概率不超過0.25的前提下認為喜歡閱讀古典文學與性別有關系?
(2)為引導學生積極參與閱讀古典文學書籍,語文教研組計劃牽頭舉辦雅禮教育集團古典文學閱讀交流會.經過綜合考慮與對比,語文教研組已經從這200人中篩選出了5名男生代表和4名女生代表,其中有3名男生代表和2名女生代表喜歡古典文學.現從這9名代表中任選3名男生代表和2名女生代表參加交流會,記![]() 為參加交流會的5人中喜歡古典文學的人數,求
為參加交流會的5人中喜歡古典文學的人數,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
附: ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求證:數列![]() 為等比數列;
為等比數列;
(2)設數列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() 為定值;
為定值;
(3)判斷數列![]() 中是否存在三項成等差數列,并證明你的結論.
中是否存在三項成等差數列,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,其焦距為
,其焦距為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,
上,![]() ,直線
,直線![]() 的斜率為
的斜率為![]() (
(![]() 為半焦距)·
為半焦距)·
(1)求橢圓![]() 的方程;
的方程;
(2)設圓![]() 的切線
的切線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點(
兩點(![]() 為坐標原點),求證:
為坐標原點),求證:![]() ;
;
(3)在(2)的條件下,求![]() 的最大值
的最大值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com