
【題目】為吸引顧客,某公司在商場舉辦電子游戲活動.對于![]() 兩種游戲,每種游戲玩一次均會出現兩種結果,而且每次游戲的結果相互獨立,具體規則如下:玩一次游戲
兩種游戲,每種游戲玩一次均會出現兩種結果,而且每次游戲的結果相互獨立,具體規則如下:玩一次游戲![]() ,若綠燈閃亮,獲得
,若綠燈閃亮,獲得![]() 分,若綠燈不閃亮,則扣除
分,若綠燈不閃亮,則扣除![]() 分(即獲得
分(即獲得![]() 分),綠燈閃亮的概率為
分),綠燈閃亮的概率為![]() ;玩一次游戲
;玩一次游戲![]() ,若出現音樂,獲得
,若出現音樂,獲得![]() 分,若沒有出現音樂,則扣除
分,若沒有出現音樂,則扣除![]() 分(即獲得
分(即獲得![]() 分),出現音樂的概率為
分),出現音樂的概率為![]() .玩多次游戲后累計積分達到
.玩多次游戲后累計積分達到![]() 分可以兌換獎品.
分可以兌換獎品.
(1)記![]() 為玩游戲
為玩游戲![]() 和
和![]() 各一次所得的總分,求隨機變量
各一次所得的總分,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(2)記某人玩![]() 次游戲
次游戲![]() ,求該人能兌換獎品的概率.
,求該人能兌換獎品的概率.
【答案】(1)詳見解析;(2)![]() .
.
【解析】試題分析:(1)隨機變量![]() 可取的數值為
可取的數值為![]() ,每一種情況為兩種游戲的結果的概率的乘積,求出概率再求分布列和期望;(2)每次得60分的概率為
,每一種情況為兩種游戲的結果的概率的乘積,求出概率再求分布列和期望;(2)每次得60分的概率為![]() ,扣20分的概率為
,扣20分的概率為![]() ,設需出現
,設需出現![]() 次音樂,那么
次音樂,那么![]() ,計算
,計算![]() 值,再求其概率.
值,再求其概率.
試題解析:(1)隨機變量![]() 的所有可能取值為
的所有可能取值為![]() ,分別對應以下四種情況:
,分別對應以下四種情況:
①玩游戲![]() ,綠燈閃亮,且玩游戲
,綠燈閃亮,且玩游戲![]() ,出現音樂;
,出現音樂;
②玩游戲![]() ,綠燈不閃亮,且玩游戲
,綠燈不閃亮,且玩游戲![]() ,出現音樂;
,出現音樂;
③玩游戲![]() ,綠燈閃亮,且玩游戲
,綠燈閃亮,且玩游戲![]() ,沒有出現音樂;
,沒有出現音樂;
④玩游戲![]() ,綠燈不閃亮,且玩游戲
,綠燈不閃亮,且玩游戲![]() ,沒有出現音樂,
,沒有出現音樂,
所以![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
即![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
![]() .
.
(2)設某人玩![]() 次游戲
次游戲![]() 的過程中,出現音樂
的過程中,出現音樂![]() 次,則沒出現音樂
次,則沒出現音樂![]() 次,依題意得
次,依題意得![]() ,解得
,解得![]() ,所以
,所以![]() 或
或![]() 或
或![]() .
.
設“某人玩![]() 次游戲
次游戲![]() 能兌換獎品”為事件
能兌換獎品”為事件![]() ,
,
則![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)的長軸是短軸的兩倍,點P(
=1(a>b>0)的長軸是短軸的兩倍,點P( ![]() ,
, ![]() )在橢圓上,不過原點的直線l與橢圓相交于A、B兩點,設直線OA、l、OB的斜率分別為k1、k、k2 , 且k1、k、k2恰好構成等比數列,記△AOB的面積為S.
)在橢圓上,不過原點的直線l與橢圓相交于A、B兩點,設直線OA、l、OB的斜率分別為k1、k、k2 , 且k1、k、k2恰好構成等比數列,記△AOB的面積為S. 
(1)求橢圓C的方程;
(2)試判斷|OA|2+|OB|2是否為定值?若是,求出這個值;若不是,請說明理由?
(3)求△AOB面積S的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)=x2+2(a﹣1)x+2在區間[﹣1,2]上單調,則實數a的取值范圍為( )
A.[2,+∞)
B.(﹣∞,﹣1]
C.(﹣∞,﹣1]∪[2,+∞)
D.(﹣∞,﹣1)∪(2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校![]() 屆高三文(1)班在一次數學測驗中,全班
屆高三文(1)班在一次數學測驗中,全班![]() 名學生的數學成績的頻率分布直方圖如下,已知分數在
名學生的數學成績的頻率分布直方圖如下,已知分數在![]() 的學生數有
的學生數有![]() 人.
人.
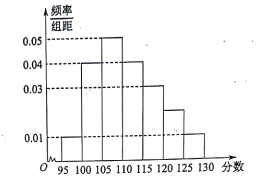
(1)求總人數![]() 和分數在
和分數在![]() 的人數
的人數![]() ;
;
(2)利用頻率分布直方圖,估算該班學生數學成績的眾數和中位數各是多少?
(3)現在從比分數在![]() 名學生(男女生比例為
名學生(男女生比例為![]() )中任選
)中任選![]() 人,求其中至多含有
人,求其中至多含有![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .直線
.直線![]() 交曲線
交曲線![]() 于
于![]() 兩點.
兩點.
(1)寫出直線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的直角坐標為
的直角坐標為![]() ,求點
,求點![]() 到
到![]() 兩點的距離之積.
兩點的距離之積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y= ![]() +lg(﹣x2+4x﹣3)的定義域為M,
+lg(﹣x2+4x﹣3)的定義域為M,
(1)求M;
(2)當x∈M時,求函數f(x)=a2x+2+34x(a<﹣3)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B、C是橢圓M: ![]() =1(a>b>0)上的三點,其中點A的坐標為
=1(a>b>0)上的三點,其中點A的坐標為 ![]() ,BC過橢圓M的中心,且
,BC過橢圓M的中心,且 ![]() .
.
(1)求橢圓M的方程;
(2)過點(0,t)的直線l(斜率存在時)與橢圓M交于兩點P、Q,設D為橢圓M與y軸負半軸的交點,且 ![]() ,求實數t的取值范圍.
,求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com