
如圖,已知橢圓 過點(diǎn)
過點(diǎn)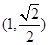 ,離心率為
,離心率為 ,左、右焦點(diǎn)分別為
,左、右焦點(diǎn)分別為 、
、 .點(diǎn)
.點(diǎn) 為直線
為直線 上且不在
上且不在 軸上的任意一點(diǎn),直線
軸上的任意一點(diǎn),直線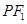 和
和 與橢圓的交點(diǎn)分別為
與橢圓的交點(diǎn)分別為 、
、 和
和 、
、 ,
, 為坐標(biāo)原點(diǎn).設(shè)直線
為坐標(biāo)原點(diǎn).設(shè)直線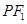 、
、 的斜率分別為
的斜率分別為 、
、 .
.

(i)證明: ;
;
(ii)問直線 上是否存在點(diǎn)
上是否存在點(diǎn) ,使得直線
,使得直線 、
、 、
、 、
、 的斜率
的斜率 、
、 、
、 、
、 滿足
滿足 ?若存在,求出所有滿足條件的點(diǎn)
?若存在,求出所有滿足條件的點(diǎn) 的坐標(biāo);若不存在,說明理由.
的坐標(biāo);若不存在,說明理由.
(1)根據(jù)橢圓的方程以及斜率公式來得到求解。
(2)點(diǎn)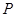 的坐標(biāo)為
的坐標(biāo)為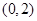 或
或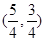
【解析】
試題分析:(i).橢圓方程為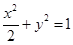 ,
,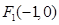 、
、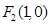 設(shè)
設(shè)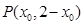
則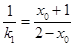 ,
,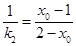 ,
, 2分
2分
(ii)記A、B、C、D坐標(biāo)分別為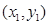 、
、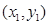 、
、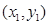 、
、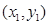
設(shè)直線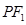 :
: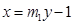
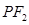 :
: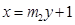
聯(lián)立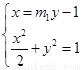 可得
可得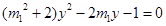 4分
4分
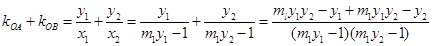
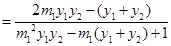 ,代入
,代入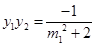 ,
,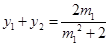 可得
可得
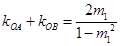 6分
6分
同理,聯(lián)立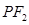 和橢圓方程,可得
和橢圓方程,可得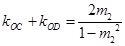 7分
7分
由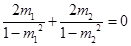 及
及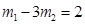 (由(i)得)可解得
(由(i)得)可解得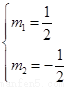 ,或
,或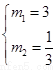 ,所以直線方程為
,所以直線方程為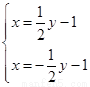 或
或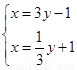 ,
,
所以點(diǎn)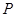 的坐標(biāo)為
的坐標(biāo)為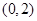 或
或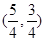 10分
10分
考點(diǎn):橢圓方程
點(diǎn)評:主要是考查了直線與橢圓的位置關(guān)系,以及運(yùn)用韋達(dá)定理求解斜率和,進(jìn)而得到直線的方程,得到點(diǎn)P的坐標(biāo),屬于中檔題。


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優(yōu)秀生快樂假期每一天全新寒假作業(yè)本系列答案
優(yōu)秀生快樂假期每一天全新寒假作業(yè)本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分12分)
如圖,已知橢圓![]() 過點(diǎn)
過點(diǎn)![]() ,兩個焦點(diǎn)分別為
,兩個焦點(diǎn)分別為![]() ,
,![]() 為坐標(biāo)原點(diǎn),平行于
為坐標(biāo)原點(diǎn),平行于![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于不同的兩點(diǎn)
于不同的兩點(diǎn)![]() ,
,
(Ⅰ)求橢圓![]() 的方程;
的方程;
 (Ⅱ)試問直線
(Ⅱ)試問直線![]() 的斜率之和是否為定值,若為定值,求出以線段
的斜率之和是否為定值,若為定值,求出以線段![]() 為直徑且過點(diǎn)
為直徑且過點(diǎn)![]() 的圓的方程;若不存在,說明理由.
的圓的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆安徽省毫州市高二上學(xué)期質(zhì)量檢測理科數(shù)學(xué) 題型:解答題
如圖,已知橢圓 過點(diǎn).
過點(diǎn). ,離心率為
,離心率為 ,左、右焦點(diǎn)分別為
,左、右焦點(diǎn)分別為 、
、 .點(diǎn)
.點(diǎn) 為直線
為直線 上且不在
上且不在 軸上的任意一點(diǎn),直線
軸上的任意一點(diǎn),直線 和
和 與橢圓的交點(diǎn)分別為
與橢圓的交點(diǎn)分別為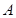 、
、 和
和 、
、 ,
, 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).
(I)求橢圓的標(biāo)準(zhǔn)方程;
(II)設(shè)直線 、
、 的斜線分別為
的斜線分別為 、
、 . 證明:
. 證明:

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年普通高等學(xué)校招生全國統(tǒng)一考試(山東卷)文科數(shù)學(xué)全解全析 題型:解答題
(本小題滿分14分)
如圖,已知橢圓
 過點(diǎn)(1,
過點(diǎn)(1, ),離心率為
),離心率為  ,左右焦點(diǎn)分別為
,左右焦點(diǎn)分別為 .點(diǎn)
.點(diǎn) 為直線
為直線 :
: 上且不在
上且不在 軸上的任意一點(diǎn),直線
軸上的任意一點(diǎn),直線 和
和 與橢圓的交點(diǎn)分別為
與橢圓的交點(diǎn)分別為 和
和 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).

(Ⅰ)求橢圓的標(biāo)準(zhǔn)方程;
(Ⅱ)設(shè)直線 、
、 斜率分別為
斜率分別為
 .
.
(ⅰ)證明:
(ⅱ )問直線 上是否存在一點(diǎn)
上是否存在一點(diǎn) ,使直線
,使直線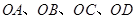 的斜率
的斜率 滿足
滿足 ?若存在,求出所有滿足條件的點(diǎn)
?若存在,求出所有滿足條件的點(diǎn) 的坐標(biāo);若不存在,說明理由.
的坐標(biāo);若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年高考試題(山東卷)解析版(文) 題型:解答題
如圖,已知橢圓
 過點(diǎn)(1,
過點(diǎn)(1, ),離心率為
),離心率為
 ,左右焦點(diǎn)分別為
,左右焦點(diǎn)分別為 .點(diǎn)
.點(diǎn) 為直線
為直線 :
: 上且不在
上且不在 軸上的任意一點(diǎn),直線
軸上的任意一點(diǎn),直線 和
和 與橢圓的交點(diǎn)分別為
與橢圓的交點(diǎn)分別為 和
和 為坐標(biāo)原點(diǎn).
為坐標(biāo)原點(diǎn).
 (Ⅰ) 求橢圓的標(biāo)準(zhǔn)方程;
(Ⅰ) 求橢圓的標(biāo)準(zhǔn)方程;
(Ⅱ)設(shè)直線 、
、 斜率分別為
斜率分別為
 .
.
 證明:
證明:
(ⅱ)問直線 上是否存在一點(diǎn)
上是否存在一點(diǎn) ,
,
使直線 的斜率
的斜率
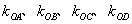 滿足
滿足 ?若存在,求出所有滿足條件的點(diǎn)
?若存在,求出所有滿足條件的點(diǎn) 的坐標(biāo);若不存在,說明理由.
的坐標(biāo);若不存在,說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com