
某單位有 、
、 、
、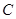 三個工作點,需要建立一個公共無線網絡發射點
三個工作點,需要建立一個公共無線網絡發射點 ,使得發射點到三個工作點的距離相等.已知這三個工作點之間的距離分別為
,使得發射點到三個工作點的距離相等.已知這三個工作點之間的距離分別為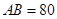
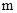 ,
,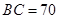
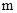 ,
,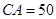
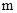 .假定
.假定 、
、 、
、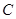 、
、 四點在同一平面上.
四點在同一平面上.
(1)求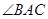 的大小;
的大小;
(2)求點 到直線
到直線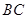 的距離.
的距離.
(1)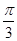 ;(2)
;(2)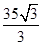 m
m
解析試題分析:(1)先確定 的三條邊長,然后利用余弦定理求
的三條邊長,然后利用余弦定理求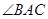 的大小;(2)方法1:先利用點
的大小;(2)方法1:先利用點 到三點
到三點 、
、 、
、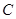 的距離相等將點
的距離相等將點 視為
視為 外接圓的圓心,利用正弦定理先算出
外接圓的圓心,利用正弦定理先算出 外接圓的半徑,然后再構造直角三角形借助勾股定理計算點
外接圓的半徑,然后再構造直角三角形借助勾股定理計算點 到直線
到直線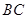 的距離;方法2:先利用點
的距離;方法2:先利用點 到三點
到三點 、
、 、
、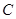 的距離相等將點
的距離相等將點 視為
視為 外接圓的圓心,直接利用銳角三角函數計算點
外接圓的圓心,直接利用銳角三角函數計算點 到直線
到直線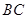 的距離.
的距離.
試題解析:方法1:因為發射點 到
到 、
、 、
、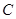 三個工作點的距離相等,
三個工作點的距離相等,
所以點 為△
為△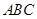 外接圓的圓心. 5分
外接圓的圓心. 5分
設外接圓的半徑為 ,
,
在△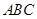 中,由正弦定理得
中,由正弦定理得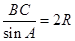 , 7分
, 7分
因為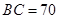 ,由(1)知
,由(1)知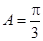 ,所以
,所以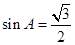 .
.
所以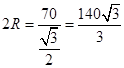 ,即
,即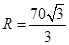 . 8分
. 8分
過點 作邊
作邊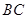 的垂線,垂足為
的垂線,垂足為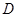 , 9分
, 9分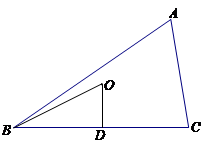
在△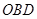 中,
中,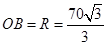 ,
,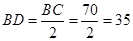 ,
,
所以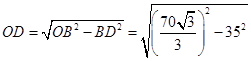 11分
11分 .
.
所以點 到直線
到直線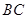 的距離為
的距離為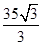
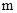 . 12分
. 12分
方法2:因為發射點 到
到 、
、 、
、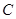 三個工作點的距離相等,
三個工作點的距離相等,
所以點 為△
為△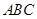 外接圓的圓心. 5分
外接圓的圓心. 5分
連結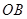 ,
,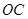 ,
,
過點 作邊
作邊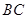 的垂線,垂足為
的垂線,垂足為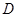 , 6分
, 6分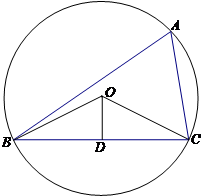
由(1)知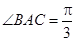 ,所以
,所以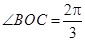 .
.
所以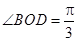 . 9分
. 9分
在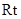 △
△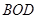 中,
中,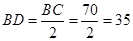 ,
,
所以

科目:高中數學 來源: 題型:解答題
已知函數f(x)=sin2ωx+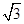 sinωxcosωx(ω>0)的最小正周期為π,
sinωxcosωx(ω>0)的最小正周期為π,
(Ⅰ)求ω的值及函數f(x)的單調增區間;
(Ⅱ)求函數f(x)在[0,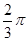 ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知向量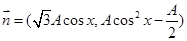 ,
, ,
,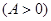 ,函數
,函數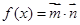 的最大值為
的最大值為 .
.
(Ⅰ)求 ;
;
(Ⅱ)將函數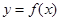 的圖像向左平移
的圖像向左平移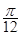 個單位,再將所得圖像上各點的橫坐標縮短為原來的
個單位,再將所得圖像上各點的橫坐標縮短為原來的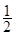 倍,縱坐標不變,得到函數
倍,縱坐標不變,得到函數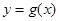 的圖像,求
的圖像,求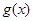 在
在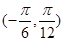 上的值域.
上的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com