
【題目】已知![]() (
(![]() ).
).
(Ⅰ)求證:![]() ;
;
(Ⅱ)若不等式![]() 在
在![]() 時恒成立,求最小正整數
時恒成立,求最小正整數![]() ,并給出證明.
,并給出證明.
【答案】(1)見解析(2)最小正整數![]() 等于5.
等于5.
【解析】試題分析:(1)利用分析法證不等式:兩邊平方,整理轉化,再平方即得已知事實(2)先逐個代入驗證并歸納猜想最小正整數![]() .再利用數學歸納法進行證明: 當
.再利用數學歸納法進行證明: 當![]() 時,利用放縮及歸納假設得
時,利用放縮及歸納假設得![]() ,即可證明
,即可證明
試題解析:證明:(Ⅰ)要證:![]()
即證:![]()
只需證:![]()
即證:![]()
只需證:![]()
只需證:![]()
上式顯然成立
![]() 不等式
不等式![]() 成立.
成立.
(Ⅱ)![]() 即
即 ![]()
當![]() 時,左邊=
時,左邊=![]() ,右邊=
,右邊=![]() ,不等式不成立;
,不等式不成立;
當![]() 時,左邊=
時,左邊=![]() ,右邊=
,右邊=![]() ,不等式不成立;
,不等式不成立;
當![]() 時,左邊=
時,左邊=![]() ,右邊=
,右邊=![]() ,不等式不成立;
,不等式不成立;
當![]() 時,左邊=
時,左邊=![]() ,右邊=
,右邊=![]() ,不等式不成立;
,不等式不成立;
當![]() 時,左邊=
時,左邊=![]() ,右邊=
,右邊=![]() ,不等式成立;
,不等式成立;
當![]() 時,左邊=
時,左邊=![]() ,右邊=
,右邊=![]() ,不等式成立;
,不等式成立;
故猜想最小正整數![]() .
.
下面證明![]() 時
時![]() 成立:
成立:
證法一:(數學歸納法)
①當![]() 時,左邊=
時,左邊=![]() ,右邊=
,右邊=![]() ,不等式成立
,不等式成立
②假設當![]() 時,不等式成立,即
時,不等式成立,即![]() ,
,
則當![]() 時,
時,![]()
當![]() 時,顯然
時,顯然![]()
故![]()
即![]() 時不等式成立
時不等式成立
綜上,不等式![]() 在
在![]() 時恒成立,且最小正整數
時恒成立,且最小正整數![]() 等于5.
等于5.
證法二:當![]() 時,
時,
由![]()
得![]()
![]()
即![]()
所以,不等式![]() 在
在![]() 時恒成立,且最小正整數
時恒成立,且最小正整數![]() 等于5.
等于5.


科目:高中數學 來源: 題型:
【題目】在![]() 中,根據下列條件解三角形,其中有兩個解的是( )
中,根據下列條件解三角形,其中有兩個解的是( )
A. b="10," A=450, C=600 B. a=6, c=5, B=600
C. a=7, b=5, A=600 D. a=14, b="16," A=450
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下列命題:
有下列命題:
①函數![]() 的圖象關于
的圖象關于![]() 軸對稱;
軸對稱;
②在區間![]() 上,函數
上,函數![]() 是減函數;
是減函數;
③在區間![]() 上,函數
上,函數![]() 是增函數;
是增函數;
④函數![]() 的值域是
的值域是![]() .其中正確命題序號為____.
.其中正確命題序號為____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【湖南省2017屆高三長郡中學、衡陽八中等十三校重點中學第一次聯考數學(理)】
已知函數![]() .
.
(1)當![]() 時,試求函數圖像過點
時,試求函數圖像過點![]() 的切線方程;
的切線方程;
(2)當![]() 時,若關于
時,若關于![]() 的方程
的方程![]() 有唯一實數解,試求實數
有唯一實數解,試求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 有兩個極值點
有兩個極值點![]() ,且不等式
,且不等式![]() 恒成立,試求實數
恒成立,試求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() 為實數.
為實數.
(1)若關于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() ,求實數
,求實數![]() 的值;
的值;
(2)設![]() ,當
,當![]() 時,求函數
時,求函數![]() 的最小值(用
的最小值(用![]() 表示);
表示);
(3)若關于![]() 不等式
不等式![]() 的解集中恰好有兩個整數解,求
的解集中恰好有兩個整數解,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】齊王與田忌賽馬,田忌的上等馬優于齊王的中等馬,劣于齊王的上等馬,田忌的中等馬優于齊王的下等馬,劣于齊王的中等馬,田忌的下等馬劣于齊王的下等馬,現從雙方的馬匹中隨機選一匹進行一場比賽,則田忌馬獲勝的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫藥研究所開發了一種新藥,如果成年人按規定的劑量服用,據監測,服藥后每毫升血液中的含藥量![]() (微克)與時間
(微克)與時間![]() (小時)之間的關系近似滿足如圖所示的曲線.
(小時)之間的關系近似滿足如圖所示的曲線.
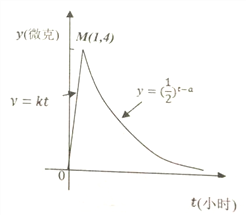
(1)寫出服藥后![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)據進一步測定:每毫升血液中含藥量不少于0.25微克時,治療疾病有效.求服藥一次治療疾病的有效時間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com