
【題目】知函數f(x)=ax2﹣2x+lnx(a≠0,a∈R).
(1)判斷函數 f (x)的單調性;
(2)若函數 f (x)有兩個極值點x1,x2,求證:f(x1)+f(x2)<﹣3.
【答案】(1)見解析(2)見解析
【解析】試題分析:(1)求出函數的導數,通過討論![]() 的范圍,分別令
的范圍,分別令![]() 得增區間,
得增區間, ![]() 得減區間;(2)求出
得減區間;(2)求出![]() ,令
,令![]() ,利用導數研究函數的單調性,求出
,利用導數研究函數的單調性,求出![]() 的最大值即可證明.
的最大值即可證明.
試題解析:(1)由題意得,函數f(x)的定義域是(0,+∞),
f′(x)=2ax﹣2+![]() =
=![]() ,
,
令g(x)=2ax2﹣2x+1,△=4﹣8a,
①a≥![]() 時,△=4﹣8a≤0,f′(x)≥0恒成立,
時,△=4﹣8a≤0,f′(x)≥0恒成立,
則f(x)在(0,+∞)遞增;
②a<![]() 時,△=4﹣8a>0,
時,△=4﹣8a>0,
由g(x)=0,解得:x1=![]() ,x2=
,x2=![]() ,
,
(i)0<a<![]() 時,0<x1<x2,
時,0<x1<x2,
此時f(x)在區間(x1,x2)遞減,在(0,x1),(x2,+∞)遞增;
(ii)a<0時,x2<0<x1,
此時f(x)在區間(x1,+∞)遞減,在(0,x1)遞增,
∴a≥![]() 時,f(x)在(0,+∞)遞增,
時,f(x)在(0,+∞)遞增,
0<a<![]() 時,f(x)在區間(x1,x2)遞減,在(0,x1),(x2,+∞)遞增,
時,f(x)在區間(x1,x2)遞減,在(0,x1),(x2,+∞)遞增,
a<0時,f(x)在區間(x1,+∞)遞減,在(0,x1)遞增;
(2)證明:由(1)得0<a<![]() 時,函數f(x)有2個極值點x1,x2,
時,函數f(x)有2個極值點x1,x2,
且x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴f(x1)+f(x2)=﹣(lna+![]() )﹣(1+ln2),
)﹣(1+ln2),
令h(a)=﹣(lna+![]() )﹣(1+ln2),(0<a<
)﹣(1+ln2),(0<a<![]() ),
),
則h′(a)=﹣(![]() ﹣
﹣![]() )=
)=![]() >0,
>0,
∴h(a)在(0,![]() )遞增,
)遞增,
則h(a)<h(![]() )=﹣(ln
)=﹣(ln![]() +2)﹣(1+ln2)=﹣3,
+2)﹣(1+ln2)=﹣3,
即f(x1)+f(x2)<﹣3.


科目:高中數學 來源: 題型:
【題目】為了解某社區居民的家庭年收入所年支出的關系,隨機調查了該社區5戶家庭,得到如表統計數據表:
收入x (萬元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y (萬元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根據如表可得回歸直線方程y= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,據此估計,該社區一戶收入為20萬元家庭年支出為( )
,據此估計,該社區一戶收入為20萬元家庭年支出為( )
A.11.4萬元
B.11.8萬元
C.15.2萬元
D.15.6萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,曲線![]() 的普通方程為
的普通方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 、
、![]() 的極坐標方程;
的極坐標方程;
(2)求曲線![]() 與
與![]() 交點的極坐標,其中
交點的極坐標,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+ ![]() +lnx,a∈R.
+lnx,a∈R.
(1)當a=1時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(2)若f(x)在區間(1,4)內單調遞增,求a的取值范圍;
(3)討論函數g(x)=f′(x)﹣x的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數f(x)=lg ![]() (x≠0,x∈R)有下列命題:
(x≠0,x∈R)有下列命題:
①函數y=f(x)的圖象關于y軸對稱;
②在區間(﹣∞,0)上,函數y=f(x)是減函數;
③函數f(x)的最小值為lg2;
④在區間(1,+∞)上,函數f(x)是增函數.
其中正確命題序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2x2﹣4x+a,g(x)=logax(a>0且a≠1).
(1)若函數f(x)在[﹣1,2m]上不具有單調性,求實數m的取值范圍;
(2)若f(1)=g(1).
(ⅰ)求實數a的值;
(ⅱ)設 ![]() ,t2=g(x),
,t2=g(x), ![]() ,當x∈(0,1)時,試比較t1 , t2 , t3的大小.
,當x∈(0,1)時,試比較t1 , t2 , t3的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】20名學生某次數學考試成績(單位:分)的頻率分布直方圖如圖: 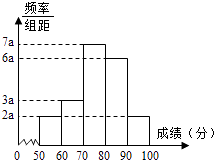
(1)求頻率分布直方圖中a的值;
(2)分別求出成績落在[50,60)與[60,70)中的學生人數;
(3)從成績在[50,70)的學生任選2人,求此2人的成績都在[60,70)中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com