
已知函數
 .
.
(Ⅰ)若 在
在 處的切線垂直于直線
處的切線垂直于直線 ,求該點的切線方程,并求此時函數
,求該點的切線方程,并求此時函數 的單調區間;
的單調區間;
(Ⅱ)若 對任意的
對任意的 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
(Ⅰ) 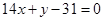 ,
, 的單調遞增區間是
的單調遞增區間是 ;單調遞減區間是
;單調遞減區間是 和
和 ;
;
(Ⅱ) 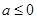 或
或 .
.
解析試題分析:(Ⅰ)通過切線垂直直線可以得到切線的斜率,解出 ,將
,將 代入求出切點坐標,從而求出切線方程,令
代入求出切點坐標,從而求出切線方程,令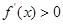 和
和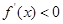 分別求出函數的單調遞增區間和遞減區間;(Ⅱ)通過對
分別求出函數的單調遞增區間和遞減區間;(Ⅱ)通過對 的討論,求出
的討論,求出 在
在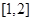 上的最大值,令
上的最大值,令 ,解出
,解出 的取值范圍.
的取值范圍.
試題解析:(Ⅰ)  ,根據題意
,根據題意 ,解得
,解得 ,
,
此時切點坐標是 ,故所求的切線方程是
,故所求的切線方程是 ,即
,即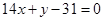 .
.
當 時,
時,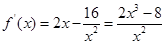 ,
,
令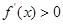 ,解得
,解得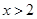 ,令
,令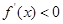 ,解得
,解得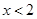 且
且 ,故函數
,故函數 的單調遞增區間是
的單調遞增區間是 ;單調遞減區間是
;單調遞減區間是 和
和 . 5分
. 5分
(Ⅱ) 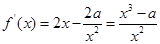 .
.
①若 ,則
,則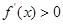 在區間
在區間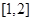 上恒成立,
上恒成立, 在區間
在區間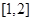 上單調遞增,函數
上單調遞增,函數 在區間
在區間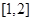 上的最大值為
上的最大值為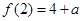 ; 7分
; 7分
②若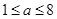 ,則在區間
,則在區間 上
上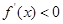 ,函數單調遞減,在區間
,函數單調遞減,在區間 上
上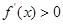 ,函數單調遞增,故函數
,函數單調遞增,故函數 在區間
在區間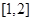 上的最大值為
上的最大值為 ,
,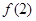 中的較大者,
中的較大者, ,故當
,故當 時,函數的最大值為
時,函數的最大值為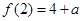 ,當
,當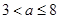 時,函數的最大值為
時,函數的最大值為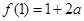 ; 9分
; 9分
③當 時,
時,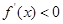 在區間
在區間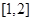 上恒成立,函數
上恒成立,函數 在區間
在區間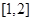 上單調遞減,函數的最大值為
上單調遞減,函數的最大值為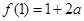 . 11分
. 11分
綜上可知,在區間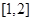 上,當
上,當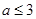 時,函數
時,函數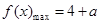 ,當
,當 時,函數
時,函數 .
.
不等式 對任意的
對任意的 恒成立等價于在區間
恒成立等價于在區間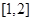 上,
上, ,故當
,故當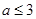 時,
時,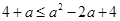 ,即
,即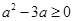 ,解得
,解得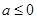 或
或 ;當
;當 時,
時, ,即
,即


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:高中數學 來源: 題型:解答題
預計某地區明年從年初開始的前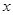 個月內,對某種商品的需求總量
個月內,對某種商品的需求總量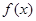 (萬件)近似滿足:
(萬件)近似滿足: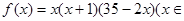 N*,且
N*,且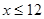 )
)
(1)寫出明年第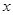 個月的需求量
個月的需求量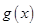 (萬件)與月份
(萬件)與月份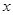 的函數關系式,并求出哪個月份的需求量超過
的函數關系式,并求出哪個月份的需求量超過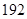 萬件;
萬件;
(2)如果將該商品每月都投放到該地區 萬件(不包含積壓商品),要保證每月都滿足供應,
萬件(不包含積壓商品),要保證每月都滿足供應, 應至少為多少萬件?(積壓商品轉入下月繼續銷售)
應至少為多少萬件?(積壓商品轉入下月繼續銷售)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數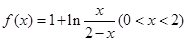 .
.
(1)是否存在點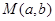 ,使得函數
,使得函數 的圖像上任意一點P關于點M對稱的點Q也在函數
的圖像上任意一點P關于點M對稱的點Q也在函數 的圖像上?若存在,求出點M的坐標;若不存在,請說明理由;
的圖像上?若存在,求出點M的坐標;若不存在,請說明理由;
(2)定義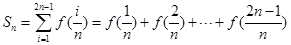 ,其中
,其中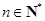 ,求
,求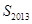 ;
;
(3)在(2)的條件下,令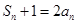 ,若不等式
,若不等式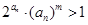 對
對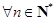 且
且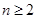 恒成立,求實數
恒成立,求實數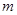 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 ,點
,點 為一定點,直線
為一定點,直線 分別與函數
分別與函數 的圖象和
的圖象和 軸交于點
軸交于點 ,
, ,記
,記 的面積為
的面積為 .
.
(I)當 時,求函數
時,求函數 的單調區間;
的單調區間;
(II)當 時, 若
時, 若 ,使得
,使得 , 求實數
, 求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數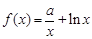 ,
,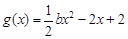 ,
,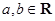
⑴求函數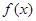 的單調區間;
的單調區間;
⑵記函數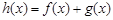 ,當
,當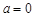 時,
時,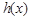 在
在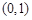 上有且只有一個極值點,求實數
上有且只有一個極值點,求實數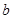 的取值范圍;
的取值范圍;
⑶記函數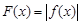 ,證明:存在一條過原點的直線
,證明:存在一條過原點的直線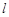 與
與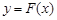 的圖象有兩個切點
的圖象有兩個切點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com