【題目】已知某運動員每次投籃命中的概率都為40%.現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率：先由計算器算出0到9之間取整數值的隨機數，指定1，2，3，4表示命中，5，6，7，8，9，0表示不命中；再以每三個隨機數為一組，代表三次投籃的結果.經隨機模擬產生了20組隨機數：
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計，該運動員三次投籃恰有兩次命中的概率為（ ）
A.0.35B.0.25C.0.20D.0.15
科目：高中數學 來源： 題型：
【題目】在一個特定時段內，以點E為中心的7n mile以內海域被設為警戒水域.點E正北55n mile處有一個雷達觀測站A，某時刻測得一艘勻速直線行駛的船只位于點A北偏東45°且與點A相距40
n mile的位置B，經過40分鐘又測得該船已行駛到點A北偏東
(其中
，
)且與點A相距10
n mile的位置C．
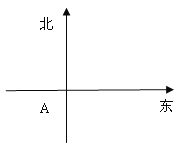
（I）求該船的行駛速度（單位：n mile /h）;
（II）若該船不改變航行方向繼續行駛.判斷它是否會進入警戒水域，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題正確的是（ ）
A.復數z1，z2的模相等，則z1，z2是共軛復數
B.z1，z2都是復數，若z1＋z2是虛數，則z1不是z2的共軛復數
C.復數z是實數的充要條件是z＝
(是z的共軛復數)
D.已知復數z1＝－1＋2i，z2＝1－i，z3＝3－2i(i是虛數單位)，它們對應的點分別為A，B，C，O為坐標原點，若
(x，y∈R)，則x＋y＝1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國古代著名的
周髀算經
中提到：凡八節二十四氣，氣損益九寸九分六分分之一；冬至晷
長一丈三尺五寸，夏至晷長一尺六寸
意思是：一年有二十四個節氣，每相鄰兩個節氣之間的日影長度差為
分；且“冬至”時日影長度最大，為1350分；“夏至”時日影長度最小，為160分則“立春”時日影長度為
A. 
分B. 
分C. 
分D. 
分
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中正確的個數有（ ）
①向量
與
是共線向量，則A、B、C、D四點必在一直線上；②單位向量都相等；③任一向量與它的相反向量不相等；④共線的向量，若起點不同，則終點一定不同．
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓E：
的離心率是
，
，
分別為橢圓E的左右頂點，B為上頂點，
的面積為
直線l過點
且與橢圓E交于P，Q兩點．
求橢圓E的標準方程；
求
面積的最大值；
設直線
與直線
交于點N，證明：點N在定直線上，并寫出該直線方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知中心在原點，焦點在x軸上的橢圓C的離心率為
，且經過點M(1，
），過點P(2,1）的直線l與橢圓C相交于不同的兩點A，B.
（1）求橢圓C的方程；
（2）是否存在直線l，滿足
？若存在，求出直線l的方程；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某高級中學今年高一年級招收“國際班”學生
人，學校為這些學生開辟了直升海外一流大學的綠色通道，為了逐步提高這些學生與國際教育接軌的能力，將這人分為三個批次參加國際教育研修培訓，在這三個批次的學生中男、女學生人數如下表：
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在這名學生中隨機抽取
名，抽到第一批次、第二批次中女學生的概率分別是
.
（1）求
的值；
（2）為了檢驗研修的效果，現從三個批次中按分層抽樣的方法抽取
名同學問卷調查，則三個批次被選取的人數分別是多少？
（3）若從第（2）小問選取的學生中隨機選出兩名學生進行訪談，求“參加訪談的兩名同學至少有一個人來自第一批次”的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4—4：極坐標與參數方程
在平面直角坐標系
中，將曲線
(
為參數) 上任意一點
經過伸縮變換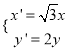
后得到曲線
的圖形．以坐標原點
為極點，x軸的非負半軸為極軸，取相同的單位長度建立極坐標系，已知直線
．
（Ⅰ）求曲線
和直線
的普通方程；
（Ⅱ）點P為曲線
上的任意一點，求點P到直線
的距離的最大值及取得最大值時點P的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
