
【題目】已知(x+ ![]() )n展開式的二項式系數之和為256
)n展開式的二項式系數之和為256
(1)求n;
(2)若展開式中常數項為 ![]() ,求m的值;
,求m的值;
(3)若展開式中系數最大項只有第6項和第7項,求m的值.
【答案】
(1)解:∵(x+ ![]() )n展開式的二項式系數之和為256,∴2n=256,解得n=8
)n展開式的二項式系數之和為256,∴2n=256,解得n=8
(2)解: ![]() 的通項公式:Tr+1=
的通項公式:Tr+1= ![]() =mr
=mr ![]() x8-2r,令8-2r=0,解得r=4.
x8-2r,令8-2r=0,解得r=4.
∴m4 ![]() =
= ![]() ,解得m=
,解得m= ![]()
(3)解: ![]() 的通項公式:Tr+1=
的通項公式:Tr+1= ![]() =mr
=mr ![]() x8-2r,
x8-2r,
∵展開式中系數最大項只有第6項和第7項,∴m≠0,
T6=m5 ![]() x-2,T7=m6
x-2,T7=m6 ![]() x-4,令
x-4,令 ![]() , 解得m=2
, 解得m=2
【解析】(1)根據二項式系數之和即可求出n的值即可。(2)根據題意首先寫出二項式的展開式令x的次數等于零即可求出r的值,進而得到m的值。(3)利用二項展開式中項的系數的之間的關系即可求出m的值即可。
【考點精析】利用二項式定理的通項公式對題目進行判斷即可得到答案,需要熟知二項式通項公式:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】學生會為了調查學生對2018年俄羅斯世界杯的關注是否與性別有關,抽樣調查100人,得到如下數據:
不關注 | 關注 | 總計 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
總計 | 75 | 25 | 100 |
根據表中數據,通過計算統計量K2= ![]() ,并參考一下臨界數據:
,并參考一下臨界數據:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此認為“學生對2018年俄羅斯年世界杯的關注與性別有關”,則此結論出錯的概率不超過( )
A.0.10
B.0.05
C.0.025
D.0.01
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分12分)已知不等式ax2-3x+6>4的解集為{x|x<1或x>b},
(1)求a,b;
(2)解不等式ax2-(ac+b)x+bc<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() ;
;
(1)若函數 ![]() 在
在 ![]() 上為增函數,求正實數
上為增函數,求正實數 ![]() 的取值范圍;
的取值范圍;
(2)當 ![]() 時,求函數
時,求函數 ![]() 在
在 ![]() 上的最值;
上的最值;
(3)當 ![]() 時,對大于1的任意正整數
時,對大于1的任意正整數 ![]() ,試比較
,試比較 ![]() 與
與 ![]() 的大小關系.
的大小關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中社團進行社會實踐,對[25,55]歲的人群隨機抽取n人進行了一次是否開通“微博”的調查,若開通“微博”的稱為“時尚族”,否則稱為“非時尚族”,通過調查分別得到如圖所示統計表和各年齡段人數頻率分布直方圖: 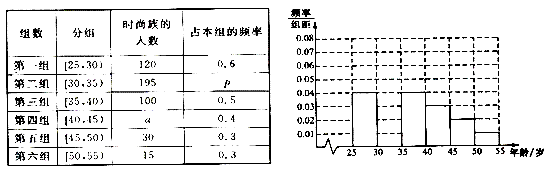
完成以下問題:
(Ⅰ)補全頻率分布直方圖并求n , a , p的值;
(Ⅱ)從[40,50)歲年齡段的“時尚族”中采用分層抽樣法抽取18人參加網絡時尚達人大賽,其中選取3人作為領隊,記選取的3名領隊中年齡在[40,45)歲的人數為X,求X的分布列和期望E(X)..
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在考試測評中,常用難度曲線圖來檢測題目的質量,一般來說,全卷得分高的學生,在某道題目上的答對率也應較高,如果是某次數學測試壓軸題的第1、2問得分難度曲線圖,第1、2問滿分均為6分,圖中橫坐標為分數段,縱坐標為該分數段的全體考生在第1、2問的平均難度,則下列說法正確的是( ) 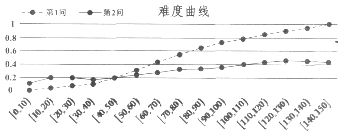
A.此題沒有考生得12分
B.此題第1問比第2問更能區分學生數學成績的好與壞
C.分數在[40,50)的考生此大題的平均得分大約為4.8分
D.全體考生第1問的得分標準差小于第2問的得分標準差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知不等式|x+3|﹣2x﹣1<0的解集為(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函數f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零點,求實數m的值.
|﹣x0(m>0)有零點,求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com