【題目】《九章算術(shù)》是我國古代內(nèi)容極為豐富的數(shù)學名著，書中有如下問題：“今有芻甍，下廣三丈，袤四丈，上袤二丈，無廣，高二丈，問：積幾何?”其意思為：“今有底面為矩形的屋脊狀的楔體，下底面寬3丈，長4丈，上棱長2丈，高2丈，問：它的體積是多少?”已知l丈為10尺，該楔體的三視圖如圖所示，其中網(wǎng)格紙上小正方形邊長為1，則該楔體的體積為（ ）
A. 10000立方尺 B. 11000立方尺
C. 12000立方尺 D. 13000立方尺
心算口算巧算一課一練系列答案
應(yīng)用題作業(yè)本系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
（
）是奇函數(shù).
（1）求實數(shù)
的值；
（2）若
，
，求
的取值范圍.
（3）若
，且
在
上
恒成立，求
的范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，（
），求
（1）
；
（2）令
，求
關(guān)于
的函數(shù)關(guān)系式，及的取值范圍.
（3）求函數(shù)
，（）的最大值和最小值；并寫出它的值域.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在正三棱柱ABC-A1B1C1中，AB=AA1=2，點P，Q分別為A1B1，BC的中點．
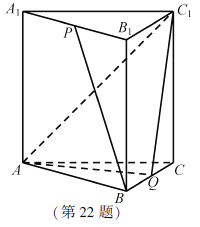
（1）求異面直線BP與AC1所成角的余弦值；
（2）求直線CC1與平面AQC1所成角的正弦值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
：
（
）的左右焦點分別為
，
且關(guān)于直線
的對稱點
在直線
上.
（1）求橢圓的離心率；
（2）若的長軸長為
且斜率為
的直線
交橢圓于
，
兩點，問是否存在定點
，使得
，
的斜率之和為定值？若存在，求出所有滿足條件的點坐標；若不存在，說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】從某保險公司的推銷員中隨機抽取50名，統(tǒng)計這些推銷員某月的月銷售額（單位：千元），由統(tǒng)計結(jié)果得如圖頻數(shù)分別表：
月銷售額 分組 | [12.25，14.75） | [14.75，17.25） | [17.25，19.75） | [19.75，22.25） | [22.25，24.75） |
頻數(shù) | 4 | 10 | 24 | 8 | 4 |
（1）作出這些數(shù)據(jù)的頻率分布直方圖；
（2）估計這些推銷員的月銷售額的平均數(shù)（同一組中的數(shù)據(jù)用該組區(qū)間的中點作代表）；
（3）根據(jù)以上抽樣調(diào)查數(shù)據(jù)，公司將推銷員的月銷售指標確定為17.875千元，試判斷是否有60%的職工能夠完成該銷售指標．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在棱長為1正方體
中，點
，
分別為邊
，
的中點，將
沿
所在的直線進行翻折，將
沿
所在直線進行翻折，在翻折的過程中，下列說法錯誤的是（ ）
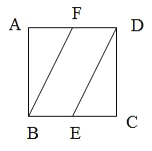
A. 無論旋轉(zhuǎn)到什么位置，
、
兩點都不可能重合
B. 存在某個位置，使得直線
與直線
所成的角為
C. 存在某個位置，使得直線與直線所成的角為
D. 存在某個位置，使得直線
與直線
所成的角為
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知在四棱錐
中， 
為正三角形， 
，底面
為平行四邊形，平面
平面
，點
是側(cè)棱
的中點，平面
與棱
交于點
.
(1)求證： 
；
(2)若
，求平面
與平面
所成二面角（銳角）的余弦值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
