
【題目】某社區為豐富居民節日活動,組織了“迎新春”象棋大賽,已知報名的選手情況統計如下表:
組別 | 男 | 女 | 總計 |
中年組 |
|
| 91 |
老年組 | 16 |
|
|
已知中年組女性選手人數是僅比老年組女性選手人數多2人,若對中年組和老年組分別利用分層抽樣的方法抽取部分報名者參加比賽,已知老年組抽取了5人,其中女性3人,中年組抽取了7人.
(1)求表格中的數據![]() ;
;
(2)若從選出的中年組的選手中隨機抽取兩名進行比賽,求至少有一名女性選手的概率.
【答案】(Ⅰ)見解析(Ⅱ)![]() .
.
【解析】試題分析:(Ⅰ)由題意,老年組中,女性抽取了3人,則男性抽取了2人,利用分層抽樣的比例,即可求解![]() 的值;
的值;
(Ⅱ)由已知得中年組抽取男性![]() 人;女性2人,列舉出基本事件的個數,利用古典概型的概率計算公式,即可求解至少有一名女性的概率.
人;女性2人,列舉出基本事件的個數,利用古典概型的概率計算公式,即可求解至少有一名女性的概率.
試題解析:
(Ⅰ)由題意,老年組中,女性抽取了3人,則男性抽取了2人,故抽樣比為![]() .
.
所以![]() .
.
故![]() .
.
所以![]() ,
,![]() .
.
(Ⅱ)由已知,中年組共抽取了7人,所以抽樣比為![]() .
.
所以中年組抽取男性![]() 人;女性2人.
人;女性2人.
記5名男性分別為![]() ,2名女性分別為
,2名女性分別為![]() .
.
則從中隨機選取兩名,不同的結果為:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
共21種.
其中至少有一名女性的選法為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共11種.
.共11種.
所以至少有一名女性的概率為![]() .
.


科目:高中數學 來源: 題型:
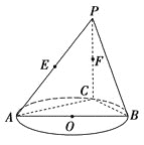
【題目】如圖,AB是圓O的直徑,點C是圓O上異于A,B的點,直線PC⊥平面ABC,E,F分別是PA,PC的中點.
(1)記平面BEF與平面ABC的交線為l,試判斷直線l與平面PAC的位置關系,并加以證明;
(2)設AB=PC=2,BC=1,求三棱錐P-BEF的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為零的等差數列{an}中,a1=1且a1 , a3 , a9成等比數列, (Ⅰ)求數列{an}的通項公式
(Ⅱ)設bn=n2 ![]() 求數列[bn}的前n項和Sn .
求數列[bn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某公司的職工食堂中,食堂每天以3元/個的價格從面包店購進面包,然后以5元/個的價格出售.如果當天賣不完,剩下的面包以1元/個的價格賣給飼料加工廠.根據以往統計資料,得到食堂每天面包需求量的頻率分布直方圖如圖所示.食堂某天購進了 90個面包,以![]() (個)(其中
(個)(其中![]() )表示面包的需求量,
)表示面包的需求量, ![]() (元)表示利潤.
(元)表示利潤.
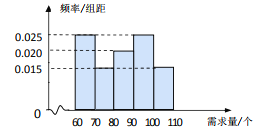
(1)根據直方圖計算需求量的中位數;
(2)估計利潤![]() 不少于100元的概率;
不少于100元的概率;
(3)在直方圖的需求量分組中,以需求量落入該區間的頻率作為需求量在該區間的概率,求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)與y軸的交點為A,B(點A位于點B的上方),F為左焦點,原點O到直線FA的距離為
=1(a>b>0)與y軸的交點為A,B(點A位于點B的上方),F為左焦點,原點O到直線FA的距離為 ![]() b.
b.
(1)求橢圓C的離心率;
(2)設b=2,直線y=kx+4與橢圓C交于不同的兩點M,N,求證:直線BM與直線AN的交點G在定直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某聯歡晚會舉行抽獎活動,舉辦方設置了甲、乙兩種抽獎方案,方案甲的中獎率為 ![]() ,中獎可以獲得2分;方案乙的中獎率為P0(0<P0<1),中獎可以獲得3分;未中獎則不得分.每人有且只有一次抽獎機會,每次抽獎中獎與否互不影響,晚會結束后憑分數兌換獎品. (Ⅰ)張三選擇方案甲抽獎,李四選擇方案乙抽獎,記他們的累計得分為X,若X≤3的概率為
,中獎可以獲得2分;方案乙的中獎率為P0(0<P0<1),中獎可以獲得3分;未中獎則不得分.每人有且只有一次抽獎機會,每次抽獎中獎與否互不影響,晚會結束后憑分數兌換獎品. (Ⅰ)張三選擇方案甲抽獎,李四選擇方案乙抽獎,記他們的累計得分為X,若X≤3的概率為 ![]() ,求P0;
,求P0;
(Ⅱ)若張三、李四兩人都選擇方案甲或都選擇方案乙進行抽獎,問:他們選擇何種方案抽獎,累計得分的數學期望較大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中裝著標有數字1、2、3、4、5的小球各2個,從袋中任取3個小球,每個小球被取出的可能性都相等,用ξ表示取出的3個小球上的最大數字,求:
(1)取出的3個小球上的數字互不相同的概率;
(2)隨機變量ξ的概率分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com