
【題目】如圖,在△ABC中,AB=AC,BC=2, ![]() ,
, ![]() ,若
,若 ![]() ,則
,則 ![]() = .
= . 
【答案】﹣ ![]()
【解析】解:以BC的中點O為原點,BC所在直線為x軸建立直角坐標系,如圖所示.
則B(﹣1,0),C(1,0),
設A(0,m),由題意得D( ![]() ,
, ![]() m),E(-
m),E(- ![]() ,
, ![]() m),
m),
∴ ![]() =(
=( ![]() ,
, ![]() m),
m), ![]() =(1,﹣m),
=(1,﹣m),
∵ ![]() ,
,
∴ ![]() ×1+
×1+ ![]() m×(﹣m)=﹣
m×(﹣m)=﹣ ![]() ,解之得m=2(負值舍去)
,解之得m=2(負值舍去)
由此可得E(- ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ),
), ![]() =(﹣1,﹣2)
=(﹣1,﹣2)
∴ ![]() =﹣
=﹣ ![]() ×(﹣1)+
×(﹣1)+ ![]() ×(﹣2)=﹣
×(﹣2)=﹣ ![]() .
.
故答案為:﹣ ![]()
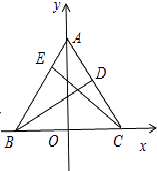
以BC的中點O為原點,建立如圖所示直角坐標系,可得B(﹣1,0),C(1,0).設A(0,m),從而算出向量 ![]() 的坐標關于m的式子,由
的坐標關于m的式子,由 ![]() 建立關于m的方程,解出m=2.由此算出
建立關于m的方程,解出m=2.由此算出 ![]() 的坐標,從而可得
的坐標,從而可得 ![]() 的值.
的值.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:
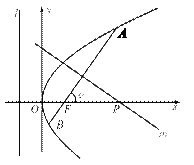
【題目】已知拋物線![]() 上一點
上一點![]() 到焦點
到焦點![]() 的距離
的距離![]() ,傾斜角
,傾斜角
為![]() 的直線經過焦點
的直線經過焦點![]() ,且與拋物線交于
,且與拋物線交于![]() 、
、![]() 兩點.
兩點.
(1)求拋物線的標準方程及準線![]() 的方程;
的方程;
(2)若![]() 為銳角,作線段
為銳角,作線段![]() 的垂直平分線
的垂直平分線![]() 交
交![]() 軸于點
軸于點![]() ,證明
,證明![]() 為定值,并求此定值.
為定值,并求此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等比數列{an}中,a1=1,且a2是a1與a3﹣1的等差中項.
(1)求數列{an}的通項公式;
(2)若數列{bn}滿足 ![]() .求數列{bn}的前n項和
.求數列{bn}的前n項和 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足 ![]() ,記數列{an}的前n項和為Sn , cn=Sn﹣2n+2ln(n+1)
,記數列{an}的前n項和為Sn , cn=Sn﹣2n+2ln(n+1)
(1)令 ![]() ,證明:對任意正整數n,|sin(bnθ)|≤bn|sinθ|
,證明:對任意正整數n,|sin(bnθ)|≤bn|sinθ|
(2)證明數列{cn}是遞減數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sinωxcosωx+ ![]() cos2ωx﹣
cos2ωx﹣ ![]() (ω>0),直線x=x1 , x=x2是y=f(x)圖象的任意兩條對稱軸,且|x1﹣x2|的最小值為
(ω>0),直線x=x1 , x=x2是y=f(x)圖象的任意兩條對稱軸,且|x1﹣x2|的最小值為 ![]() .
.
(1)求f(x)的表達式;
(2)將函數f(x)的圖象向右平移 ![]() 個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到函數y=g(x)的圖象,若關于x的方程g(x)+k=0,在區間
個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到函數y=g(x)的圖象,若關于x的方程g(x)+k=0,在區間 ![]() 上有且只有一個實數解,求實數k的取值范圍.
上有且只有一個實數解,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=sinxcosx﹣cos2(x+ ![]() ).
).
(1)求f(x)的單調區間;
(2)在銳角△ABC中,角A,B,C的對邊分別為a,b,c,若f( ![]() )=0,a=1,求△ABC面積的最大值.
)=0,a=1,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 是[1,∞]上的增函數.當實數m取最大值時,若存在點Q,使得過Q的直線與曲線y=g(x)圍成兩個封閉圖形,且這兩個封閉圖形的面積總相等,則點Q的坐標為( )
是[1,∞]上的增函數.當實數m取最大值時,若存在點Q,使得過Q的直線與曲線y=g(x)圍成兩個封閉圖形,且這兩個封閉圖形的面積總相等,則點Q的坐標為( )
A.(0,﹣3)
B.(0,3)
C.(0,﹣2)
D.(0,2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題中:
①某地市高三理科學生有15000名,在一次調研測試中,數學成績 ![]() 服從正態分布
服從正態分布 ![]() ,已知
,已知 ![]() ,若按成績分層抽樣的方式抽取100份試卷進行分析,則應從120分以上(包括120分)的試卷中抽取
,若按成績分層抽樣的方式抽取100份試卷進行分析,則應從120分以上(包括120分)的試卷中抽取 ![]() 份;
份;
②已知命題 ![]() ,則
,則 ![]() :
: ![]() ;
;
③在 ![]() 上隨機取一個數
上隨機取一個數 ![]() ,能使函數
,能使函數 ![]() 在
在 ![]() 上有零點的概率為
上有零點的概率為 ![]() ;
;
④設 ![]() ,則“
,則“ ![]() ”是“
”是“ ![]() ”的充要條件.
”的充要條件.
其中真命題的序號為.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com