【題目】在正三棱柱ABCA1B1C1中，已知AB＝1，AA1＝2，E，F，G分別是棱AA1，AC和A1C1的中點，以
為正交基底，建立如圖所示的空間直角坐標系F-xyz.
（1）求異面直線AC與BE所成角的余弦值；
（2）求二面角F-BC1-C的余弦值．
【答案】（1）
.（2）
.
【解析】
（1）先根據空間直角坐標系，求得向量
和向量
的坐標，再利用線線角的向量方法求解.
（2）分別求得平面BFC1的一個法向量和平面BCC1的一個法向量，再利用面面角的向量方法求解.
規范解答 （1） 因為AB＝1，AA1＝2，則F(0，0，0)，A
，C
，B
，E
，
所以＝(－1，0，0)，＝
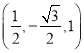
記異面直線AC和BE所成角為α，
則cosα＝|cos〈
〉|＝
＝，
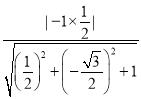所以異面直線AC和BE所成角的余弦值為.
（2） 設平面BFC1的法向量為
= (x1，y1，z1)．
因為
＝，
＝
，
則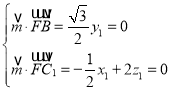
取x1＝4，得平面BFC1的一個法向量為＝(4，0，1)．
設平面BCC1的法向量為
＝(x2，y2，z2)．
因為
＝
，
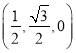＝(0，0，2)，
則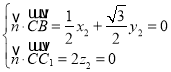
取x2＝
得平面BCC1的一個法向量為＝(，－1，0)，
所以cos〈
〉＝
=
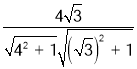根據圖形可知二面角F-BC1-C為銳二面角，
所以二面角F-BC1-C的余弦值為.
科目：高中數學 來源： 題型：
【題目】設橢圓
（
）的左右頂點為
，上下頂點為
，菱形
的內切圓
的半徑為
，橢圓的離心率為
.
（1）求橢圓
的方程；
（2）設
是橢圓上關于原點對稱的兩點，橢圓上一點
滿足
，試判斷直線
與圓的位置關系，并證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P－ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP＝AB＝AD＝1．
（Ⅰ）若直線PB與CD所成角的大小為
，求BC的長；
（Ⅱ）求二面角B－PD－A的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，以正四棱錐VABCD的底面中心O為坐標原點建立空間直角坐標系Oxyz，其中Ox∥BC，Oy∥AB，E為VC的中點．正四棱錐的底面邊長為2a，高為h，且有cos〈
，
〉＝－
.
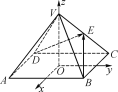
（1）求
的值；
（2）求二面角B-VC-D的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是某公司一種產品的日銷售量
（單位：百件）關于日最高氣溫
（單位：
）的散點圖.
數據：
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
（1）請剔除一組數據，使得剩余數據的線性相關性最強，并用剩余數據求日銷售量關于日最高氣溫的線性回歸方程
；
（2）根據現行《重慶市防暑降溫措施管理辦法》.若氣溫超過36度，職工可享受高溫補貼.已知某日該產品的銷售量為53.1，請用（1）中求出的線性回歸方程判斷該公司員工當天是否可享受高溫補貼？
附：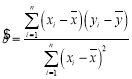
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
：
的焦距為
，直線
（
）與交于兩個不同的點
、
，且
時直線
與的兩條漸近線所圍成的三角形恰為等邊三角形.
（1）求雙曲線的方程；
（2）若坐標原點
在以線段
為直徑的圓的內部，求實數
的取值范圍；
（3）設
、
分別是的左、右兩頂點，線段
的垂直平分線交直線于點
，交直線
于點
，求證：線段
在
軸上的射影長為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知首項為
的數列
各項均為正數，且
，
.
(1)若數列
的通項
滿足
，且
，求數列的前n項和為
；
(2)若數列
的通項
滿足
，前n項和為
，當數列是等差數列時，對任意的，均存在
，使得
成立，求滿足條件的所有整數構成的集合.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，
為橢圓E：
的左、右焦點，過點
的直線l與橢圓E有且只有一個交點T．
（1）求
面積的取值范圍．
（2）若有一束光線從點射出，射在直線l上的T點上，經過直線l反射后，試問反射光線是否恒過定點？若是，請求出該定點；若否，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
