
【題目】已知橢圓![]() 的離心率
的離心率![]() ,橢圓
,橢圓![]() 上的點到其左焦點
上的點到其左焦點![]() 的最大距離為
的最大距離為![]() .
.
(1)求橢圓的標(biāo)準(zhǔn)方程;
(2)過橢圓![]() 左焦點
左焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線與直線
的垂線與直線![]() 交于點
交于點![]() ,求
,求![]() 的最小值和此時直線
的最小值和此時直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)最小值為
;(2)最小值為![]() ,此時直線
,此時直線![]() 的方程為
的方程為![]() .
.
【解析】
(1)根據(jù)橢圓![]() 上的點到其左焦點的最大距離為
上的點到其左焦點的最大距離為![]() ,得到
,得到![]() ,再由
,再由![]() ,聯(lián)立求解即可.
,聯(lián)立求解即可.
(2)①當(dāng)直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 的方程為
的方程為![]() ,可分別求導(dǎo)T,A,B的坐標(biāo),然后利用兩點間距離公式求解;②當(dāng)直線
,可分別求導(dǎo)T,A,B的坐標(biāo),然后利用兩點間距離公式求解;②當(dāng)直線![]() 的斜率存在時,設(shè)直線
的斜率存在時,設(shè)直線![]() 的方程為
的方程為![]() ,由
,由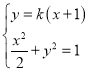 ,利用弦長公式求得
,利用弦長公式求得![]() ,再由
,再由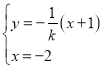 ,求得交點
,求得交點![]() ,從而得到
,從而得到![]() ,代入
,代入![]() 求解.
求解.
(1)由題可知![]() ,又橢圓
,又橢圓![]() 上的點到其左焦點的最大距離為
上的點到其左焦點的最大距離為![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,
∴![]() ,
,
所以橢圓![]() 的方程為
的方程為![]() .
.
(2)①當(dāng)直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 的方程為
的方程為![]() ,則
,則![]() ,
,
所以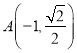 ,
,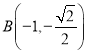 ,此時
,此時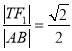 ;
;
②當(dāng)直線![]() 的斜率存在時,設(shè)直線
的斜率存在時,設(shè)直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]()
由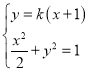 ,
,
得![]() ,
,
由韋達定理得![]() ,
,![]() ,
,
則![]() ,
,
聯(lián)立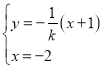 ,可得
,可得![]() ,
,
所以![]()
所以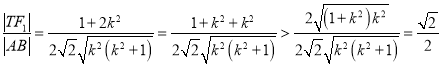 .
.
因為![]() 所以等號不成立.
所以等號不成立.
綜上,![]() 的最小值為
的最小值為![]() ,此時直線
,此時直線![]() 的方程為
的方程為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】“雜交水稻之父”袁隆平一生致力于雜交水稻技術(shù)的研究、應(yīng)用與推廣,發(fā)明了“三系法”秈型雜交水稻,成功研究出“兩系法”雜交水稻,創(chuàng)建了超級雜交稻技術(shù)體系,為我國糧食安全、農(nóng)業(yè)科學(xué)發(fā)展和世界糧食供給做出了杰出貢獻;某雜交水稻種植研究所調(diào)查某地水稻的株高,得出株高(單位:cm)服從正態(tài)分布,其密度曲線函數(shù)為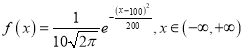 ,則下列說法正確的是( )
,則下列說法正確的是( )
A.該地水稻的平均株高為100cm
B.該地水稻株高的方差為10
C.隨機測量一株水稻,其株高在120cm以上的概率比株高在70cm以下的概率大
D.隨機測量一株水稻,其株高在(80,90)和在(100,110)(單位:cm)的概率一樣大
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】湖北七市州高三5月23日聯(lián)考后,從全體考生中隨機抽取44名,獲取他們本次考試的數(shù)學(xué)成績![]() 和物理成績
和物理成績![]() ,繪制成如圖散點圖:
,繪制成如圖散點圖:
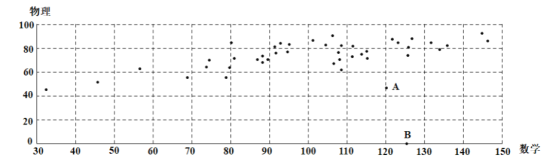
根據(jù)散點圖可以看出![]() 與
與![]() 之間有線性相關(guān)關(guān)系,但圖中有兩個異常點
之間有線性相關(guān)關(guān)系,但圖中有兩個異常點![]() .經(jīng)調(diào)查得知,
.經(jīng)調(diào)查得知,![]() 考生由于重感冒導(dǎo)致物理考試發(fā)揮失常,
考生由于重感冒導(dǎo)致物理考試發(fā)揮失常,![]() 考生因故未能參加物理考試.為了使分析結(jié)果更科學(xué)準(zhǔn)確,剔除這兩組數(shù)據(jù)后,對剩下的數(shù)據(jù)作處理,得到一些統(tǒng)計的值:
考生因故未能參加物理考試.為了使分析結(jié)果更科學(xué)準(zhǔn)確,剔除這兩組數(shù)據(jù)后,對剩下的數(shù)據(jù)作處理,得到一些統(tǒng)計的值:![]()
![]()
![]() 其中
其中![]() ,
,![]() 分別表示這42名同學(xué)的數(shù)學(xué)成績、物理成績,
分別表示這42名同學(xué)的數(shù)學(xué)成績、物理成績,![]() ,2,…,42,
,2,…,42,![]() 與
與![]() 的相關(guān)系數(shù)
的相關(guān)系數(shù)![]() .
.
(1)若不剔除![]() 兩名考生的數(shù)據(jù),用44組數(shù)據(jù)作回歸分析,設(shè)此時
兩名考生的數(shù)據(jù),用44組數(shù)據(jù)作回歸分析,設(shè)此時![]() 與
與![]() 的相關(guān)系數(shù)為
的相關(guān)系數(shù)為![]() .試判斷
.試判斷![]() 與
與![]() 的大小關(guān)系,并說明理由;
的大小關(guān)系,并說明理由;
(2)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程,并估計如果
的線性回歸方程,并估計如果![]() 考生參加了這次物理考試(已知
考生參加了這次物理考試(已知![]() 考生的數(shù)學(xué)成績?yōu)?/span>125分),物理成績是多少?
考生的數(shù)學(xué)成績?yōu)?/span>125分),物理成績是多少?
(3)從概率統(tǒng)計規(guī)律看,本次考試七市州的物理成績![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,以剔除后的物理成績作為樣本,用樣本平均數(shù)
,以剔除后的物理成績作為樣本,用樣本平均數(shù)![]() 作為
作為![]() 的估計值,用樣本方差
的估計值,用樣本方差![]() 作為
作為![]() 的估計值.試求七市州共50000名考生中,物理成績位于區(qū)間(62.8,85.2)的人數(shù)
的估計值.試求七市州共50000名考生中,物理成績位于區(qū)間(62.8,85.2)的人數(shù)![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
附:①回歸方程![]() 中:
中: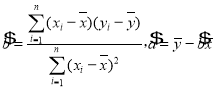
②若![]() ,則
,則![]()
③![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點
的焦點![]() 到準(zhǔn)線
到準(zhǔn)線![]() 的距離為2,直線
的距離為2,直線![]() 與拋物線交于不同的兩點
與拋物線交于不同的兩點![]() ,
,![]() .
.
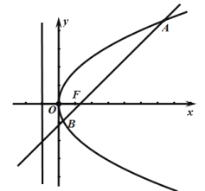
(1)求拋物線的方程;
(2)是否存在與![]() 的取值無關(guān)的定點
的取值無關(guān)的定點![]() ,使得直線
,使得直線![]() ,
,![]() 的斜率之和恒為定值?若存在,求出所有點
的斜率之和恒為定值?若存在,求出所有點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題共l4分)
已知函數(shù)f(x)=![]() x +
x +![]() , h(x)=
, h(x)=![]() .
.
(I)設(shè)函數(shù)F(x)=f(x)一h(x),求F(x)的單調(diào)區(qū)間與極值;
(Ⅱ)設(shè)a∈R,解關(guān)于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《算法統(tǒng)宗》是中國古代數(shù)學(xué)名著,由明代數(shù)學(xué)家程大位編著,它對我國民間普及珠算和數(shù)學(xué)知識起到了很大的作用,是東方古代數(shù)學(xué)的名著.在這部著作中,許多數(shù)學(xué)問題都是以歌訣形式呈現(xiàn)的,“九兒問甲歌”就是其中一首:“一個公公九個兒,若問生年總不知,自長排來差三歲,共年二百又零七,借問長兒多少歲,各兒歲數(shù)要詳推.”這首歌決的大意是:“一位老公公有九個兒子,九個兒子從大到小排列,相鄰兩人的年齡差三歲,并且兒子們的年齡之和為207歲,請問大兒子多少歲,其他幾個兒子年齡如何推算.”在這個問題中,記這位公公的第![]() 個兒子的年齡為
個兒子的年齡為![]() ,則
,則![]() ( )
( )
A.17B.29C.23D.35
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以坐標(biāo)原點O為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線C1的極坐標(biāo)方程為:
軸的正半軸為極軸建立極坐標(biāo)系,曲線C1的極坐標(biāo)方程為:![]() ,曲線C2的參數(shù)方程為:
,曲線C2的參數(shù)方程為: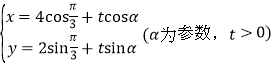 ,點N的極坐標(biāo)為
,點N的極坐標(biāo)為![]() .
.
(Ⅰ)若M是曲線C1上的動點,求M到定點N的距離的最小值;
(Ⅱ)若曲線C1與曲線C2有有兩個不同交點,求正數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知四錐![]() 中,
中,![]() ,底面ABCD為形,
,底面ABCD為形,![]() ,點E為的AD中點.
,點E為的AD中點.
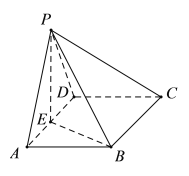
(1)證明:平面![]() 平面PBE;
平面PBE;
(2)若![]() ,二面角
,二面角![]() 的余弦值為
的余弦值為![]() ,且
,且![]() ,求PE的長.
,求PE的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義域為R的奇函數(shù)![]() ,滿足
,滿足 ,則下列敘述正確的為( )
,則下列敘述正確的為( )
①存在實數(shù)k,使關(guān)于x的方程![]() 有7個不相等的實數(shù)根
有7個不相等的實數(shù)根
②當(dāng)![]() 時,恒有
時,恒有![]()
③若當(dāng)![]() 時,
時,![]() 的最小值為1,則
的最小值為1,則![]()
④若關(guān)于![]() 的方程
的方程![]() 和
和![]() 的所有實數(shù)根之和為零,則
的所有實數(shù)根之和為零,則![]()
A.①②③B.①③C.②④D.①②③④
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com