
【題目】設![]() 為實數,函數
為實數,函數![]() .
.
(1)求![]() 的極值;
的極值;
(2)當![]() 在什么范圍內取值時,曲線
在什么范圍內取值時,曲線![]() 與
與![]() 軸僅有一個交點?
軸僅有一個交點?
【答案】(1)極大值是![]() ,極小值是
,極小值是![]() .(2)
.(2)![]()
【解析】試題分析:
(1)首先求得導函數,然后列表考查函數的單調性,據此可得f(x)的極大值是f(-![]() )=
)=![]() +a,極小值是f(1)=a-1.
+a,極小值是f(1)=a-1.
(2)由題意結合(1)中的極值的結論可得實數a的取值范圍是![]() .
.
試題解析:
(1)f′(x)=3x2-2x-1.
令f′(x)=0,則x=-![]() 或x=1.
或x=1.
當x變化時,f′(x),f(x)的變化情況如下表:
x | (-∞,- | - | (- | 1 | (1,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 極大值 | ↘ | 極小值 | ↗ |
所以f(x)的極大值是f(-![]() )=
)=![]() +a,
+a,
極小值是f(1)=a-1.
(2)函數f(x)=x3-x2-x+a=(x-1)2(x+1)+a-1,
由此可知,x取足夠大的正數時,
有f(x)>0,x取足夠小的負數時,有f(x)<0,
曲線y=f(x)與x軸至少有一個交點.
由(1)知f(x)極大值=f(-![]() )=
)=![]() +a,
+a,
f(x)極小值=f(1)=a-1.
∵曲線y=f(x)與x軸僅有一個交點,
∴f(x)極大值<0或f(x)極小值>0,
即![]() +a<0或a-1>0,
+a<0或a-1>0,
∴a<-![]() 或a>1,
或a>1,
∴當a∈(-∞,-![]() )∪(1,+∞)時,曲線y=f(x)與x軸僅有一個交點.
)∪(1,+∞)時,曲線y=f(x)與x軸僅有一個交點.


科目:高中數學 來源: 題型:
【題目】某廠生產某種產品的月固定成本為10(萬元),每生產![]() 件,需另投入成本為
件,需另投入成本為![]() (萬元).當月產量不足30件時,
(萬元).當月產量不足30件時, ![]() (萬元);當月產量不低于30件時,
(萬元);當月產量不低于30件時, ![]() (萬元).因設備問題,該廠月生產量不超過50件.現已知此商品每件售價為5萬元,且該廠每個月生產的商品都能當月全部銷售完.
(萬元).因設備問題,該廠月生產量不超過50件.現已知此商品每件售價為5萬元,且該廠每個月生產的商品都能當月全部銷售完.
(1)寫出月利潤![]() (萬元)關于月產量
(萬元)關于月產量![]() (件)的函數解析式;
(件)的函數解析式;
(2)當月產量為多少件時,該廠所獲月利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某智能手機制作完成之后還需要依次通過三道嚴格的審核程序,已知第一道審核、第二道審核、第三道審核通過的概率分別為![]() ,每道程序是相互獨立的,且一旦審核不通過就停止審核,每部手機只有三道程序都通過才能出廠銷售.
,每道程序是相互獨立的,且一旦審核不通過就停止審核,每部手機只有三道程序都通過才能出廠銷售.
(1)求審核過程中只進行兩道程序就停止審核的概率;
(2)現有3部該智能手機進入審核,記這3部手機可以出廠銷售的部數為![]() ,求X的分布列及數學期望.
,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校射擊隊的某一選手射擊一次,其命中環數的概率如表:
命中環數 | 10環 | 9環 | 8環 | 7環 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求該選手射擊一次,
(1)命中9環或10環的概率.
(2)至少命中8環的概率.
(3)命中不足8環的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個學生在一次競賽中要回答![]() 道題是這樣產生的:從
道題是這樣產生的:從![]() 道物理題中隨機抽取
道物理題中隨機抽取![]() 道;從
道;從![]() 道化學題中隨機抽取
道化學題中隨機抽取![]() 道;從
道;從![]() 道生物題中隨機抽取
道生物題中隨機抽取![]() 道.使用合適的方法確定這個學生所要回答的三門學科的題的序號(物理題的編號為
道.使用合適的方法確定這個學生所要回答的三門學科的題的序號(物理題的編號為![]() ,化學題的編號為
,化學題的編號為![]() ,生物題的編號為
,生物題的編號為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設橢圓![]() :
: ![]() ,長軸的右端點與拋物線
,長軸的右端點與拋物線![]() :
: ![]() 的焦點
的焦點![]() 重合,且橢圓
重合,且橢圓![]() 的離心率是
的離心率是![]() .
.
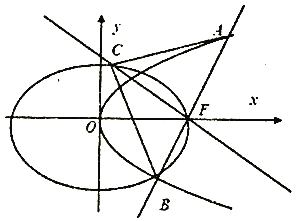
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過![]() 作直線
作直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
, ![]() 兩點,過
兩點,過![]() 且與直線
且與直線![]() 垂直的直線交橢圓
垂直的直線交橢圓![]() 于另一點
于另一點![]() ,求
,求![]() 面積的最小值,以及取到最小值時直線
面積的最小值,以及取到最小值時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com