【題目】設函數
。
（1）求函數
的單調減區間；
（2）若函數在區間
上的極大值為8，求在區間上的最小值。
【答案】（1）減區間為（﹣1，2）；（2）f(x)的最小值為-19。
【解析】
（1）先求出
，由
可得減區間；（2）根據極大值為8求得
，然后再求出最小值．
（1）f′（x）=6x2-6x﹣12=6（x-2）（x+1），
令，得﹣1＜x＜2．
∴函數f（x）的減區間為（﹣1，2）．
（2）由（1）知，f′（x）=6x2-6x﹣12=6（x+1）（x﹣2），
令f′（x）=0，得x=-1或x=2（舍）．
當x在閉區間[-2，3]變化時，f′（x），f（x）變化情況如下表
x | (-2,-1) | -1 | (-1,2) | 2 | (2,3) |
f′（x） | + | 0 | - | 0 | + |
f（x） | 單調遞增 | m+7 | 單調遞減 | m-20 | 單調遞增 |
∴當x=-1時，f（x）取極大值f（-1）=m+7，
由已知m+7=8，得m=1．
當x=2時f(x)取極小值f(2)=m-20=-19
又f(-2)=-3,
所以f(x)的最小值為-19．
全能測控一本好卷系列答案科目：高中數學 來源： 題型：
【題目】如圖，在幾何體
中，底面
為矩形，
，
，
，
.
為棱
上一點，平面
與棱
交于點
.
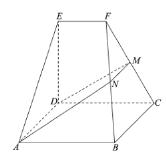
（1）求證：
；
（2）若
，試問平面
是否可能與平面
垂直？若能，求出
的值；若不能，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，直線
的參數方程為
（
為參數），其中
.以坐標原點為極點，
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
，曲線
的極坐標方程為
.
（1）求
的直角坐標方程；
（2）已知點
，與交于點
，與交于
兩點，且
，求的普通方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，圓柱的軸截面
是邊長為2的正方形，點P是圓弧
上的一動點（不與
重合），點Q是圓弧
的中點，且點
在平面的兩側.
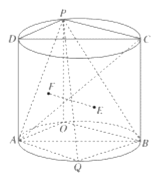
（1）證明：平面
平面
；
（2）設點P在平面
上的射影為點O，點
分別是
和
的重心，當三棱錐
體積最大時，回答下列問題.
（i）證明：
平面
；
（ii）求三棱錐
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
