
【題目】已知函數![]() ,函數
,函數![]() (
(![]() ).
).
(1)討論![]() 的單調性;
的單調性;
(2)證明:當![]() 時,
時,![]() .
.
(3)證明:當![]() 時,
時,![]() .
.
 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
【題目】某中學2018年的高考考生人數是2015年高考考生人數的![]() 倍,為了更好地對比該校考生的升學情況,統計了該校2015年和2018年的高考情況,得到如圖柱狀圖:
倍,為了更好地對比該校考生的升學情況,統計了該校2015年和2018年的高考情況,得到如圖柱狀圖:

則下列結論正確的是![]()
![]()
A. 與2015年相比,2018年一本達線人數減少
B. 與2015年相比,2018年二本達線人數增加了![]() 倍
倍
C. 2015年與2018年藝體達線人數相同
D. 與2015年相比,2018年不上線的人數有所增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 內,動點
內,動點![]() 到定點
到定點![]() 的距離與
的距離與![]() 到定直線
到定直線![]() 距離之比為
距離之比為![]() .
.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)設點![]() 是軌跡
是軌跡![]() 上兩個動點直線
上兩個動點直線![]() 與軌跡
與軌跡![]() 的另一交點分別為
的另一交點分別為![]() 且直線
且直線![]() 的斜率之積等于
的斜率之積等于![]() ,問四邊形
,問四邊形![]() 的面積
的面積![]() 是否為定值?請說明理由.
是否為定值?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn,已知:a5=2a2+3且a2,![]() ,a14成等比數列.
,a14成等比數列.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設正項數列{bn}滿足bn2Sn+1=Sn+1+2,求證:b1+b2+…+bn<n+1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,單位圓上有一點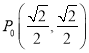 ,點
,點![]() 以點
以點![]() 為起點按逆時針方向以每秒
為起點按逆時針方向以每秒![]() 弧度作圓周運動,點
弧度作圓周運動,點![]() 的縱坐標
的縱坐標![]() 是關于時間
是關于時間![]() 的函數,記作
的函數,記作![]() .
.
(1)當![]() 時,求
時,求![]() ;
;
(2)若將函數![]() 向左平移
向左平移![]() 個單位長度后,得到的曲線關于
個單位長度后,得到的曲線關于![]() 軸對稱,求
軸對稱,求![]() 的最小正值,并求此時
的最小正值,并求此時![]() 在
在![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學棋藝協會定期舉辦“以棋會友”的競賽活動,分別包括“中國象棋”、“圍棋”、“五子棋”、“國際象棋”四種比賽,每位協會會員必須參加其中的兩種棋類比賽,且各隊員之間參加比賽相互獨立;已知甲同學必選“中國象棋”,不選“國際象棋”,乙同學從四種比賽中任選兩種參與.
(1)求甲參加圍棋比賽的概率;
(2)求甲、乙兩人參與的兩種比賽都不同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC—A1B1C1中,AA1=AC,A1B⊥AC1,設O為AC1與A1C的交點,點P為BC的中點.求證:
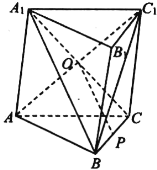
(1)OP∥平面ABB1A1;
(2)平面ACC1⊥平面OCP.
查看答案和解析>>
科目:高中數學 來源: 題型:
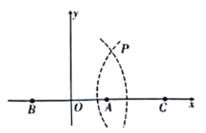
【題目】雙曲線定位法是通過測定待定點到至少三個已知點的兩個距離差所進行的一種無線電定位.通過船(待定點)接收到三個發射臺的電磁波的時間差計算出距離差,兩個距離差即可形成兩條位置雙曲線,兩者相交便可確定船位.我們來看一種簡單的“特殊”狀況;如圖所示,已知三個發射臺分別為![]() ,
,![]() ,
,![]() 且剛好三點共線,已知
且剛好三點共線,已知![]() 海里,
海里,![]() 海里,現以
海里,現以![]() 的中點為原點,
的中點為原點,![]() 所在直線為
所在直線為![]() 軸建系.現根據船
軸建系.現根據船![]() 接收到
接收到![]() 點與
點與![]() 點發出的電磁波的時間差計算出距離差,得知船
點發出的電磁波的時間差計算出距離差,得知船![]() 在雙曲線
在雙曲線![]() 的左支上,若船
的左支上,若船![]() 上接到
上接到![]() 臺發射的電磁波比
臺發射的電磁波比![]() 臺電磁波早
臺電磁波早![]() (已知電磁波在空氣中的傳播速度約為
(已知電磁波在空氣中的傳播速度約為![]() ,1海里
,1海里![]() ),則點
),則點![]() 的坐標(單位:海里)為( )
的坐標(單位:海里)為( )
A. B.
B.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com