【題目】已知橢圓
及點
，若直線
與橢圓
交于點
，且
（ 
為坐標原點），橢圓
的離心率為
.
（1）求橢圓
的標準方程；
（2）若斜率為
的直線
交橢圓
于不同的兩點
，求
面積的最大值.
【答案】(1) 
；(2)1.
【解析】試題分析： 
由橢圓的離心率公式得到
，設點
在第一象限，由橢圓的對稱性可知
，所以
，進而求得點
的坐標，然后聯立方程求得
，即可得到橢圓
的標準方程；
設直線
的方程為
，聯立橢圓方程，求得
或
，設
，求出
的值，又由題意得， 
到直線
的距離
，進而求得
面積的最大值
解析：（1）由橢圓
的離心率為
，得
，所以
.
設點
在第一象限，由橢圓的對稱性可知
，所以
，
因為點
坐標為
，所以點
坐標為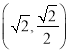
，
代入橢圓
的方程得
，與
聯立，
可得
，所以橢圓
的標準方程為
.
（2）設直線
的方程為
，由
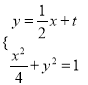得
.
由題意得， 
，
整理得
，所以
或
.
設
，則
，
所以
.
又由題意得， 
到直線
的距離
.
的面積
當且僅當
，即
時取等號，且此時滿足
，
所以
面積的最大值為1.
科目：高中數學 來源： 題型：
【題目】已知a>0，a≠1，設p：函數y＝loga(x＋3)在(0，＋∞)上單調遞減，q：函數y＝x2＋(2a－3)x＋1的圖像與x軸交于不同的兩點．如果p∨q真，p∧q假，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在學校開展的綜合實踐活動中,某班進行了小制作評比,作品上交時間為5月1日至30日,評委會把同學們上交作品的件數按照5天一組分組統計,繪制了頻率分布直方圖(如圖所示).已知從左到右各長方形的高的比為2:3:4:6:4:1,第三組的頻數為12,請解答下列各題.
(1)本次活動共有多少件作品參加評比?
(2)哪組上交的作品數量最多?有多少件?
(3)經過評比,第四組和第六組分別有10件2件作品獲獎,問這兩組哪一組獲獎率較高?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人在相同條件下各射靶10次，每次射靶的成績情況如圖所示：
（1）填寫下表：
平均數 | 方差 | 中位數 | 命中9環及以上 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 | 3 |
（2）請從四個不同的角度對這次測試進行①結合平均數和方差分析離散程度；②結合平均數和中位數分析誰的成績好些；③結合平均數和命中9環及以上的次數看誰的成績好些；④從折線圖上看兩人射靶命中環數及走勢分析誰更有潛力.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】.口袋中有質地、大小完全相同的5個球，編號分別為1，2，3，4，5，甲、乙兩人玩一種游戲：甲先摸出一個球，記下編號，放回后乙再摸一個球，記下編號，如果兩個編號的和為偶數算甲贏，否則算乙贏．
（Ⅰ）求甲贏且編號的和為6的事件發生的概率；
（Ⅱ）這種游戲規則公平嗎?試說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝4x2－kx－8.
(1)若函數y＝f(x)在區間[2,10]上單調，求實數k的取值范圍；
(2)若y＝f(x)在區間(－∞，2]上有最小值－12，求實數k的值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】把6本不同的書，全部分給甲，乙，丙三人，在下列不同情形下，各有多少種分法？（用數字作答）
(Ⅰ)甲得2本；
(Ⅱ)每人2本；
(Ⅲ)有1人4本，其余兩人各1本．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
