
【題目】已知集合A={3,a2},集合B={0,b,1﹣a},且A∩B={1},則A∪B=( )
A.{0,1,3}
B.{1,2,4}
C.{0,1,2,3}
D.{0,1,2,3,4}
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD是圓柱OO′的軸截面,點P在圓柱OO′的底面圓周上,圓柱OO′的底面圓的半徑OA=1,側面積為2π,∠AOP=60°.

(1)求證:PB⊥平面APD;
(2)是否存在點G在PD上,使得AG⊥BD;并說明理由.
(3)求三棱錐D-AGB的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,
,![]() ,
,![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,過
的左、右焦點,過![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() 、
、![]() 兩點,
兩點,![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若橢圓![]() 上存在點
上存在點![]() ,使得四邊形
,使得四邊形![]() 為平行四邊形,求此時直線
為平行四邊形,求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°. 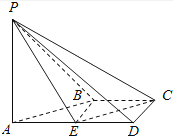
(1)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(2)若二面角P﹣CD﹣A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題中:
①命題: ![]() ;
;
②函數f(x)=2x﹣x2有三個零點;
③對(x,y)∈{(x,y)|4x+3y﹣10=0},則x2+y2≥4.
④已知函數 ![]() ,若△ABC中,角C是鈍角,那么f(sinA)>f(cosB)
,若△ABC中,角C是鈍角,那么f(sinA)>f(cosB)
其中所有真命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 C:![]() 離心率
離心率![]() ,短軸長為
,短軸長為![]() .
.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)如圖,橢圓左頂點為A,過原點O的直線![]() (與坐標軸不重合)與橢圓C交于P,Q兩點,直線PA,QA分別與y軸交于M,N兩點.試問以MN為直徑的圓是否經過定點?請證明你的結論.
(與坐標軸不重合)與橢圓C交于P,Q兩點,直線PA,QA分別與y軸交于M,N兩點.試問以MN為直徑的圓是否經過定點?請證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga![]() (a>0且a≠1)是奇函數,
(a>0且a≠1)是奇函數,
(1)求實數m的值;
(2)若a=![]() ,并且對區間[3,4]上的每一個x的值,不等式f(x)>(
,并且對區間[3,4]上的每一個x的值,不等式f(x)>(![]() )x+t恒成立,求實數t的取值范圍.
)x+t恒成立,求實數t的取值范圍.
(3)當x∈(r,a-2)時,函數f(x)的值域是(1,+∞),求實數a與r的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】砂糖橘是柑橘類的名優品種,因其味甜如砂糖故名.某果農選取一片山地種植砂糖橘,收獲時,該果農隨機選取果樹20株作為樣本測量它們每一株的果實產量(單位:kg),獲得的所有數據按照區間(40,45],(45,50],(50,55],(55,60]進行分組,得到頻率分布直方圖如圖所示.已知樣本中產量在區間(45,50]上的果樹株數是產量在區間(50,60]上的果樹株數的![]() 倍.
倍.

(1)求a,b的值;
(2)從樣本中產量在區間(50,60]上的果樹里隨機抽取兩株,求產量在區間(55,60]上的果樹至少有一株被抽中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com