
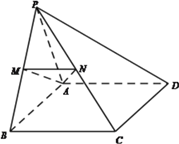
【題目】在四棱錐![]() 中,
中, ![]() 為正三角形,四邊形
為正三角形,四邊形![]() 為矩形,平面
為矩形,平面![]()
![]() 平面
平面![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點。
的中點。
(Ⅰ)求證: ![]() //平面
//平面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
【答案】(1)詳見解析;(2) ![]() .
.
【解析】試題分析:(Ⅰ)MN是△ABC的中位線,可得MN∥BC∥AD,即可證以MN∥平面PAD.
(Ⅱ)過點P作PO垂直于AB,交AB于點O,因為平面PAB⊥平面ABCD,所以PO⊥平面ABCD,如圖建立空間直角坐標系設AB=2,則A(-1,0,0),C(1,1,0),M(![]() ,0,
,0, ![]() ),B(1,0,0),N(
),B(1,0,0),N(![]() ,
,![]() ,
, ![]() ),利用向量法求解.
),利用向量法求解.
試題解析:
(Ⅰ)證明:∵M,N分別是PB,PC中點
∴MN是△ABC的中位線 ∴MN∥BC∥AD
又∵AD平面PAD,MN![]() 平面PAD
平面PAD
所以MN∥平面PAD.
(Ⅱ)過點P作PO垂直于AB,交AB于點O,
因為平面PAB⊥平面ABCD,所以PO⊥平面ABCD,
如圖建立空間直角坐標系

設AB=2,則A(-1,0,0),C(1,1,0),M(![]() ,0,
,0, ![]() ),
),
B(1,0,0),N(![]() ,
,![]() ,
, ![]() ),則
),則![]() ,
, 
設平面CAM法向量為![]() ,由
,由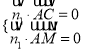 可得
可得
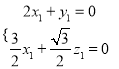 ,令
,令![]() ,則
,則![]() ,即
,即![]()
平面![]() 法向量
法向量![]()
所以,二面角![]() 的余弦值
的余弦值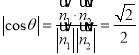
因為二面角![]() 是銳二面角,
是銳二面角,
所以二面角![]() 等于
等于![]()


科目:高中數學 來源: 題型:
【題目】2015年8月12日天津發生危化品重大爆炸事故,造成重大人員和經濟損失.某港口組織消防人員對該港口的公司的集裝箱進行安全抽檢,已知消防安全等級共分為四個等級(一級為優,二級為良,三級為中等,四級為差),該港口消防安全等級的統計結果如下表所示:

現從該港口隨機抽取了![]() 家公司,其中消防安全等級為三級的恰有20家.
家公司,其中消防安全等級為三級的恰有20家.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)按消防安全等級利用分層抽樣的方法從這![]() 家公司中抽取10家,除去消防安全等級為一級和四級的公司后,再從剩余公司中任意抽取2家,求抽取的這2家公司的消防安全等級都是二級的概率.
家公司中抽取10家,除去消防安全等級為一級和四級的公司后,再從剩余公司中任意抽取2家,求抽取的這2家公司的消防安全等級都是二級的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為做好2022年北京冬季奧運會的宣傳工作,組委會計劃從某大學選取若干大學生志愿者,某記者在該大學隨機調查了1000名大學生,以了解他們是否愿意做志愿者工作,得到的數據如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合計 | |
男大學生 | 610 | ||
女大學生 | 90 | ||
合計 | 800 |
(1) 根據題意完成表格;
(2) 是否有![]() 的把握認為愿意做志愿者工作與性別有關?
的把握認為愿意做志愿者工作與性別有關?
參考公式及數據: 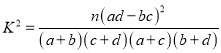 ,其中
,其中![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某智能手機制作完成之后還需要依次通過三道嚴格的審核程序,已知第一道審核、第二道審核、第三道審核通過的概率分別為![]() ,每道程序是相互獨立的,且一旦審核不通過就停止審核,每部手機只有三道程序都通過才能出廠銷售.
,每道程序是相互獨立的,且一旦審核不通過就停止審核,每部手機只有三道程序都通過才能出廠銷售.
(1)求審核過程中只進行兩道程序就停止審核的概率;
(2)現有3部該智能手機進入審核,記這3部手機可以出廠銷售的部數為![]() ,求X的分布列及數學期望.
,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校射擊隊的某一選手射擊一次,其命中環數的概率如表:
命中環數 | 10環 | 9環 | 8環 | 7環 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求該選手射擊一次,
(1)命中9環或10環的概率.
(2)至少命中8環的概率.
(3)命中不足8環的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設橢圓![]() :
: ![]() ,長軸的右端點與拋物線
,長軸的右端點與拋物線![]() :
: ![]() 的焦點
的焦點![]() 重合,且橢圓
重合,且橢圓![]() 的離心率是
的離心率是![]() .
.
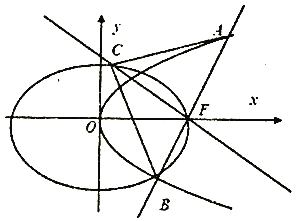
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過![]() 作直線
作直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
, ![]() 兩點,過
兩點,過![]() 且與直線
且與直線![]() 垂直的直線交橢圓
垂直的直線交橢圓![]() 于另一點
于另一點![]() ,求
,求![]() 面積的最小值,以及取到最小值時直線
面積的最小值,以及取到最小值時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com