
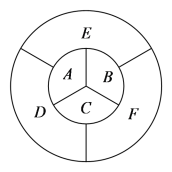
【題目】如下圖中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六個區(qū)域進行染色,每個區(qū)域只染一種顏色,每個區(qū)域只染一種顏色,且相鄰的區(qū)域不同色.若有
六個區(qū)域進行染色,每個區(qū)域只染一種顏色,每個區(qū)域只染一種顏色,且相鄰的區(qū)域不同色.若有![]() 種顏色可供選擇,則共有_________種不同的染色方案.
種顏色可供選擇,則共有_________種不同的染色方案.
【答案】![]()
【解析】
通過分析題目給出的圖形,可知要完成給出的圖形中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六個區(qū)域進行染色,最少需要
六個區(qū)域進行染色,最少需要![]() 種顏色,即
種顏色,即![]() 同色,
同色,![]() 同色,
同色,![]() 同色,由排列知識可得該類染色方法的種數(shù);也可以
同色,由排列知識可得該類染色方法的種數(shù);也可以![]() 種顏色全部用上,即
種顏色全部用上,即![]() 、
、![]() 、
、![]() 三組中有一組不同色,同樣利用排列組合知識求解該類染色方法的種數(shù),最后利用分類加法求和即可.
三組中有一組不同色,同樣利用排列組合知識求解該類染色方法的種數(shù),最后利用分類加法求和即可.
要完成給出的圖形中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 六個區(qū)域進行染色,
六個區(qū)域進行染色,
染色方法分為兩類,第一類是僅用三種顏色染色,
即![]() 同色,
同色,![]() 同色,
同色,![]() 同色,即從四種顏色中取三種顏色,有
同色,即從四種顏色中取三種顏色,有![]() 種取法,三種顏色染三個區(qū)域有
種取法,三種顏色染三個區(qū)域有![]() 種染法,共
種染法,共![]() 種染法;
種染法;
第二類是用四種顏色染色,即![]() 、
、![]() 、
、![]() 三組中有一組不同色,則有
三組中有一組不同色,則有![]() 種方案(
種方案(![]() 不同色或
不同色或![]() 不同色或
不同色或![]() 不同色),
不同色),
先從四種顏色中取兩種染同色區(qū)域有![]() 種染法,剩余兩種染在不同色區(qū)域有
種染法,剩余兩種染在不同色區(qū)域有![]() 種染法,
種染法,
共有![]() 種染法.
種染法.
由分類加法原理可得總的染色方法種數(shù)為![]() (種).
(種).
故答案為:![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】某醫(yī)務人員說:“包括我在內,我們社區(qū)診所醫(yī)生和護士共有16名.無論是否把我算在內,下面說法都是對的.在這些醫(yī)務人員中:護士多于醫(yī)生;女醫(yī)生多于女護士;女護士多于男護士;至少有一名男醫(yī)生.”請你推斷說話的人的性別與職業(yè)是( )
A.男醫(yī)生B.女醫(yī)生C.男護士D.女護士
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 且在
且在![]() 上的最大值為
上的最大值為![]() ,
,
(1)求函數(shù)f(x)的解析式;
(2)判斷函數(shù)f(x)在(0,π)內的零點個數(shù),并加以證明
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知頂點為原點的拋物線C的焦點與橢圓![]() 的上焦點重合,且過點
的上焦點重合,且過點![]() .
.
(1)求橢圓的標準方程;
(2)若拋物線上不同兩點A,B作拋物線的切線,兩切線的斜率![]() ,若記AB的中點的橫坐標為m,AB的弦長
,若記AB的中點的橫坐標為m,AB的弦長![]() ,并求
,并求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的普通方程為
的普通方程為![]() .在以坐標原點為極點,
.在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出圓![]() 的參數(shù)方程和直線
的參數(shù)方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 在
在![]() 上,點Q在
上,點Q在![]() 上,求
上,求![]() 的最小值及此時點
的最小值及此時點![]() 的直角坐標.
的直角坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .其中
.其中![]() .
.
(1)討論函數(shù)![]() 的單調性;
的單調性;
(2)函數(shù)![]() 在
在![]() 處存在極值-1,且
處存在極值-1,且![]() 時,
時,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的最大整數(shù).
的最大整數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】河北省高考綜合改革從2018年秋季入學的高一年級學生開始實施,新高考將實行“3+1+2”模式,其中3表示語文、數(shù)學、外語三科必選,1表示從物理、歷史兩科中選擇一科,2表示從化學、生物、政治、地理四科中選擇兩科.某校2018級入學的高一學生選科情況如下表:
選科組合 | 物化生 | 物化政 | 物化地 | 物生政 | 物生地 | 物政地 | 史政地 | 史政化 | 史生政 | 史地化 | 史地生 | 史化生 | 合計 |
男 | 130 | 45 | 55 | 30 | 25 | 15 | 30 | 10 | 40 | 10 | 15 | 20 | 425 |
女 | 100 | 45 | 50 | 35 | 35 | 35 | 40 | 20 | 55 | 15 | 25 | 20 | 475 |
合計 | 230 | 90 | 105 | 65 | 60 | 50 | 70 | 30 | 95 | 25 | 40 | 40 | 900 |
(1)完成下面的![]() 列聯(lián)表,并判斷是否在犯錯誤概率不超過0.01的前提下,認為“選擇物理與學生的性別有關”?
列聯(lián)表,并判斷是否在犯錯誤概率不超過0.01的前提下,認為“選擇物理與學生的性別有關”?
(2)以頻率估計概率,從該校2018級高一學生中隨機抽取3名同學,設這三名同學中選擇物理的人數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
選擇物理 | 不選擇物理 | 合計 | |
男 | 425 | ||
女 | 475 | ||
合計 | 900 |
附表及公式: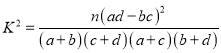
| 0.150 | 0.100 | 0.050 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程
的參數(shù)方程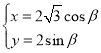 (
(![]() 為參數(shù)).直線
為參數(shù)).直線![]() 的參數(shù)方程
的參數(shù)方程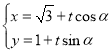 (
(![]() 為參數(shù)).
為參數(shù)).
(Ⅰ)求曲線![]() 在直角坐標系中的普通方程;
在直角坐標系中的普通方程;
(Ⅱ)以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,當曲線
軸的正半軸為極軸建立極坐標系,當曲線![]() 截直線
截直線![]() 所得線段的中點極坐標為
所得線段的中點極坐標為![]() 時,求直線
時,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() ,過其焦點
,過其焦點![]() 的直線與拋物線相交于
的直線與拋物線相交于![]() 、
、![]() 兩點,滿足
兩點,滿足![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)已知點![]() 的坐標為
的坐標為![]() ,記直線
,記直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com