
【題目】設直線![]() 與圓
與圓![]() 交于M、N兩點,且M、N關于直線
交于M、N兩點,且M、N關于直線![]() 對稱.
對稱.
(1)求m,k的值;
(2)若直線![]() 與圓C交P,Q兩點,是否存在實數a使得OP⊥OQ,如果存在,求出a的值;如果不存在,請說明理由.
與圓C交P,Q兩點,是否存在實數a使得OP⊥OQ,如果存在,求出a的值;如果不存在,請說明理由.
【答案】(1)![]() (2)不存在.
(2)不存在.
【解析】試題分析:(1)由M,N關于直線x+y=0對稱,可知所求的直線的斜率k=1,根據圓的性質可得直線y+x=0過圓的圓心C(1,m)代入可求m
(2)把x=ay+1代入(x-1)2+(y+1)2=9得(1+a2)y2+2y-8=0,設P(x1,y1),Q(x2,y2),利用韋達定理,OP⊥OQ,則有x1x2+y1y2=0,代入整理可求.
試題解析:
(1)因為圓上的兩點![]() 關于直線
關于直線![]() 對稱,所以,直線
對稱,所以,直線![]() 過圓心,圓心
過圓心,圓心![]() ,即有
,即有![]() ,同時,對稱點
,同時,對稱點![]() 的連線被對稱軸垂直平分,所以又有
的連線被對稱軸垂直平分,所以又有![]() ,從而
,從而![]()
(2)由(1)知:圓C(x-1)2+(y+1)2=9,把![]() 代入
代入![]()
得![]() ,設
,設![]() , 則
, 則![]() ,
,![]()
若![]() ,則有x1x2+y1y2=0,
,則有x1x2+y1y2=0, ![]()
![]()
![]()
即![]() , 方程無實數根,所以滿足條件的實數
, 方程無實數根,所以滿足條件的實數![]() 不存在.
不存在.


科目:高中數學 來源: 題型:
【題目】某種藥種植基地有兩處種植區的藥材需在下周一、周二兩天內采摘完畢,基地員工一天可以完成一處種植區的采摘,由于下雨會影響藥材的收益,若基地收益如下表所示:已知下周一和下周二無雨的概率相同且為![]() ,兩天是否下雨互不影響,若兩天都下雨的概率為
,兩天是否下雨互不影響,若兩天都下雨的概率為![]()

(1)求![]() 及基地的預期收益;
及基地的預期收益;
(2)若該基地額外聘請工人,可在周一當天完成全部采摘任務,若周一無雨時收益為![]() 萬元,有雨時收益為
萬元,有雨時收益為![]() 萬元,且額外聘請工人的成本為
萬元,且額外聘請工人的成本為![]() 元,問該基地是否應該額外聘請工人,請說明理由.
元,問該基地是否應該額外聘請工人,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() 為
為![]() 的中點,
的中點,![]() 為線段
為線段![]() 上的一點,且
上的一點,且![]() .現將四邊形
.現將四邊形![]() 沿直線
沿直線![]() 翻折,使翻折后的二面角
翻折,使翻折后的二面角![]() 的余弦值為
的余弦值為![]() .
.
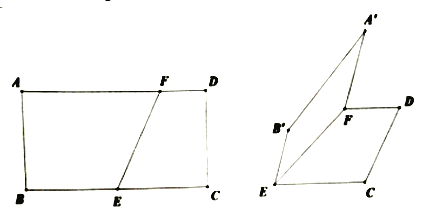
(1)求證:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如圖1,當DE∥BC時,有DBEC.(填“>”,“<”或“=”)
(2)發現探究:若將圖1中的△ADE繞點A順時針旋轉α(0°<α<180°)到圖2位置,則(1)中的結論還成立嗎?若成立,請給予證明;若不成立,請說明理由.
(3)拓展運用:如圖3,P是等腰直角三角形ABC內一點,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度數.
查看答案和解析>>
科目:高中數學 來源: 題型:
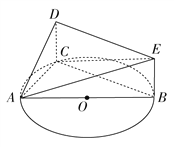
【題目】如圖,AB是圓O的直徑,點C在圓O上,矩形DCBE所在的平面垂直于圓O所在的平面, ![]() ,
, ![]() .
.
(1)若![]() ,求三棱錐
,求三棱錐![]() 的體積;
的體積;
(2)證明:平面ACD⊥平面BCDE;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】按照國家環保部發布的新修訂的《環境空氣質量標準》,規定:PM2.5的年平均濃度不得超過35微克/立方米,國家環保部門在2016年10月1日到2017年1月30日這120天對全國的PM2.5平均濃度的監測數據統計如下:
組別 | PM2.5濃度(微克/立方米) | 頻數(天) |
第一組 |
| 32 |
第二組 |
| 64 |
第三組 |
| 16 |
第四組 | 115以上 | 8 |
(1)在這120天中抽取30天的數據做進一步分析,每一組應抽取多少天?
(2)在(1)中所抽取的樣本PM2.5的平均濃度超過75(微克/立方米)的若干天中,隨機抽取2天,求恰好有一天平均濃度超過115(微克/立方米)的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com