
【題目】已知函數![]() ,
,![]() (
(![]() ).
).
(1)若曲線![]() 在
在![]() 處的切線也是曲線
處的切線也是曲線![]() 的切線,求
的切線,求![]() 的值;
的值;
(2)記![]() ,設
,設![]() 是函數
是函數![]() 的兩個極值點,且
的兩個極值點,且![]() .
.
① 若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
② 判斷函數![]() 的零點個數,并說明理由.
的零點個數,并說明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②函數
;②函數![]() 有且僅有1個零點,理由見解析
有且僅有1個零點,理由見解析
【解析】
(1)根據導數的幾何意義可求得曲線![]() 在
在![]() 處的切線方程,再聯立切線與
處的切線方程,再聯立切線與![]() ,利用判別式為0解決相切問題即可.
,利用判別式為0解決相切問題即可.
(2) ①易得![]() ,再求導根據韋達定理可知極值點滿足
,再求導根據韋達定理可知極值點滿足![]() ,再求解化簡
,再求解化簡![]() ,構造出函數
,構造出函數![]() ,求導分析函數
,求導分析函數![]() 的單調性,進而求得
的單調性,進而求得![]() 的最小值即可.
的最小值即可.
②根據①中![]() 的單調性以及極值點可知
的單調性以及極值點可知![]() ,且
,且![]() ,代入
,代入![]() 分析可知
分析可知![]() ,再根據零點存在性定理判定
,再根據零點存在性定理判定![]() ,使得
,使得![]() 即可知有1個零點.
即可知有1個零點.
(1)當![]() 時,
時,![]() ,又
,又![]() ,所以
,所以![]() ,則曲線
,則曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
由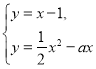 得
得![]() ,因為
,因為![]() 也是曲線
也是曲線![]() 的切線,所以
的切線,所以![]() ,
,
解之得![]() .
.
(2)①因為![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,所以
,所以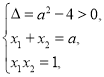 則
則![]() .
.
因為![]() ,所以
,所以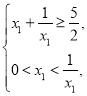 解得
解得![]() .
.
所以![]()
![]()
![]()
![]() .
.
設![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上單調遞減,當
上單調遞減,當![]() 時,
時,![]() ,
,
所以![]() ,即所求
,即所求![]() 的取值范圍為
的取值范圍為![]() .
.
② 由①知當![]() 時,
時,![]() ,
,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() ,
,![]() 單調遞減,當
單調遞減,當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
又![]() ,且由①知
,且由①知![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() ,
,![]() ,則
,則![]() ,
,
所以當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
所以當![]() 時,
時,![]() ,則當
,則當![]() 時,
時,![]() 沒有零點.
沒有零點.
因為![]() ,
,![]() ,
,![]() ,
,
又![]() 在
在![]() 上單調遞增,且圖像連續不間斷,所以
上單調遞增,且圖像連續不間斷,所以![]() ,使得
,使得![]() .
.
綜上所述,函數![]() 有且僅有1個零點.
有且僅有1個零點.


科目:高中數學 來源: 題型:
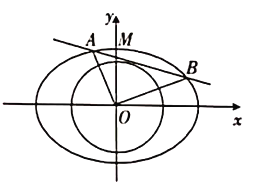
【題目】在直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() ,若圓
,若圓![]()
![]() 的一條切線與橢圓
的一條切線與橢圓![]() 有兩個交點
有兩個交點![]() ,且
,且![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)已知橢圓![]() 的上頂點為
的上頂點為![]() ,點
,點![]() 在圓
在圓![]() 上,直線
上,直線![]() 與橢圓
與橢圓![]() 相交于另一點
相交于另一點![]() ,且
,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知甲、乙、丙三個組的老年人數分別為30,30,24.現用分層抽樣的方法從中抽取14人,進行身體狀況調查.
(1)應從甲、乙、丙三個小組各抽取多少人?
(2)若抽出的14人中,10人身體狀況良好,還有4人有不同程度的狀況要進行治療,現從這14人中,再抽3人進一步了解情況,用![]() 表示抽取的3人中,身體狀況良好的人數,求
表示抽取的3人中,身體狀況良好的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線的參數方程為![]() (t為參數,α∈[0,π).以O為極點,x軸的非負半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ=ρcosθ+2,
(t為參數,α∈[0,π).以O為極點,x軸的非負半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ=ρcosθ+2,
(1)若![]() ,求直線的極坐標方程
,求直線的極坐標方程
(2)若直線與曲線C有唯一公共點,求α
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com