
【題目】如圖,在四面體ABCD中,△ABC是等邊三角形,平面ABC⊥平面ABD,點M為棱AB的中點,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求證:AD⊥BC;
(Ⅱ)求異面直線BC與MD所成角的余弦值;
(Ⅲ)求直線CD與平面ABD所成角的正弦值.

【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】分析:(Ⅰ)由面面垂直的性質定理可得AD⊥平面ABC,則AD⊥BC.
(Ⅱ)取棱AC的中點N,連接MN,ND.由幾何關系可知∠DMN(或其補角)為異面直線BC與MD所成的角.計算可得 .則異面直線BC與MD所成角的余弦值為
.則異面直線BC與MD所成角的余弦值為![]() .
.
(Ⅲ)連接CM.由題意可知CM⊥平面ABD.則∠CDM為直線CD與平面ABD所成的角.計算可得![]() .即直線CD與平面ABD所成角的正弦值為
.即直線CD與平面ABD所成角的正弦值為![]() .
.
詳解:(Ⅰ)證明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.
(Ⅱ)取棱AC的中點N,連接MN,ND.又因為M為棱AB的中點,故MN∥BC.所以∠DMN(或其補角)為異面直線BC與MD所成的角.

在Rt△DAM中,AM=1,故DM=![]() .因為AD⊥平面ABC,故AD⊥AC.
.因為AD⊥平面ABC,故AD⊥AC.
在Rt△DAN中,AN=1,故DN=![]() .
.
在等腰三角形DMN中,MN=1,可得 .
.
所以,異面直線BC與MD所成角的余弦值為![]() .
.
(Ⅲ)連接CM.因為△ABC為等邊三角形,M為邊AB的中點,故CM⊥AB,CM=![]() .又因為平面ABC⊥平面ABD,而CM
.又因為平面ABC⊥平面ABD,而CM![]() 平面ABC,故CM⊥平面ABD.所以,∠CDM為直線CD與平面ABD所成的角.
平面ABC,故CM⊥平面ABD.所以,∠CDM為直線CD與平面ABD所成的角.
在Rt△CAD中,CD=![]() =4.
=4.
在Rt△CMD中, ![]() .
.
所以,直線CD與平面ABD所成角的正弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】“H大橋”是某市的交通要道,提高過橋車輛的通行能力可改善整個城市的交通狀況.研究表明:在一般情況下,大橋上的車流速度![]() (單位:千米/小時)是車流密度
(單位:千米/小時)是車流密度![]() (單位:輛/千米)的函數,當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為
(單位:輛/千米)的函數,當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為![]() ;當車流密度不超過20輛/千米時,車流速度為60千米/小時;當
;當車流密度不超過20輛/千米時,車流速度為60千米/小時;當![]() 時,車流速度
時,車流速度![]() 是車流密度
是車流密度![]() 的一次函數.
的一次函數.
(1)當![]() 時,求函數
時,求函數![]() 的表達式.
的表達式.
(2)設車流量![]() ,求當車流密度為多少時,車流量最大?
,求當車流密度為多少時,車流量最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們把定義域為![]() 且同時滿足以下兩個條件的函數
且同時滿足以下兩個條件的函數![]() 稱為“
稱為“![]() 函數”:(1)對任意的
函數”:(1)對任意的![]() ,總有
,總有![]() ;(2)若
;(2)若![]() ,
,![]() ,則有
,則有![]() 成立,下列判斷正確的是( )
成立,下列判斷正確的是( )
A.若![]() 為“
為“![]() 函數”,則
函數”,則![]()
B.若![]() 為“
為“![]() 函數”,則
函數”,則![]() 在
在![]() 上為增函數
上為增函數
C.函數![]() 在
在![]() 上是“
上是“![]() 函數”
函數”
D.函數![]() 在
在![]() 上是“
上是“![]() 函數”
函數”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系![]() 中的一個橢圓,它的中心在原點,左焦點為
中的一個橢圓,它的中心在原點,左焦點為![]() ,右頂點為
,右頂點為![]() ,設點
,設點![]() .
.
(1)求該橢圓的標準方程;
(2)若![]() 是橢圓上的動點,求線段
是橢圓上的動點,求線段![]() 的中點
的中點![]() 的軌跡方程;
的軌跡方程;
(3)過原點![]() 的直線交橢圓于
的直線交橢圓于![]() 兩點,求
兩點,求![]() 面積的最大值,并求此時直線
面積的最大值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小張在淘寶網上開一家商店,他以10元每條的價格購進某品牌積壓圍巾2000條.定價前,小張先搜索了淘寶網上的其它網店,發現:![]() 商店以30元每條的價格銷售,平均每日銷售量為10條;
商店以30元每條的價格銷售,平均每日銷售量為10條;![]() 商店以25元每條的價格銷售,平均每日銷售量為20條.假定這種圍巾的銷售量
商店以25元每條的價格銷售,平均每日銷售量為20條.假定這種圍巾的銷售量![]() (條)是售價
(條)是售價![]() (元)
(元)![]() 的一次函數,且各個商店間的售價、銷售量等方面不會互相影響.
的一次函數,且各個商店間的售價、銷售量等方面不會互相影響.
(1)試寫出圍巾銷售每日的毛利潤![]() (元)關于售價
(元)關于售價![]() (元)
(元)![]() 的函數關系式(不必寫出定義域),并幫助小張定價,使得每日的毛利潤最高(每日的毛利潤為每日賣出商品的進貨價與銷售價之間的差價);
的函數關系式(不必寫出定義域),并幫助小張定價,使得每日的毛利潤最高(每日的毛利潤為每日賣出商品的進貨價與銷售價之間的差價);
(2)考慮到這批圍巾的管理、倉儲等費用為200元/天(只要圍巾沒有售完,均須支付200元/天,管理、倉儲等費用與圍巾數量無關),試問小張應該如何定價,使這批圍巾的總利潤最高(總利潤=總毛利潤-總管理、倉儲等費用)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著霧霾的日益嚴重,中國部分省份已經實施了“煤改氣”的計劃來改善空氣質量指數.2017年支撐我國天然氣市場消費增長的主要資源是國產常規氣和進口天然氣,資源每年的增量不足以支撐天然氣市場連續![]() 億立方米的年增量.進口LNG和進口管道氣受到接收站、管道能力和進口氣價資源的制約.未來,國產常規氣產能釋放的紅利將會逐步減弱,產量增量將維持在
億立方米的年增量.進口LNG和進口管道氣受到接收站、管道能力和進口氣價資源的制約.未來,國產常規氣產能釋放的紅利將會逐步減弱,產量增量將維持在![]() 億方以內.為了測定某市是否符合實施煤改氣計劃的標準,某監測站點于2016年8月某日起連續
億方以內.為了測定某市是否符合實施煤改氣計劃的標準,某監測站點于2016年8月某日起連續![]() 天監測空氣質量指數(AQI),數據統計如下:
天監測空氣質量指數(AQI),數據統計如下:
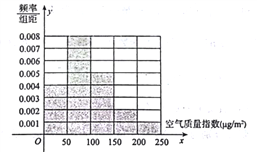
(1)根據上圖完成下列表格
空氣質量指數( |
|
|
|
|
|
天數 |
(2)計算這![]() 天中,該市空氣質量指數的平均數;
天中,該市空氣質量指數的平均數;
(3)若按照分層抽樣的方法,從空氣質量指數在![]() 以及
以及![]() 的等級中抽取
的等級中抽取![]() 天進行調研,再從這
天進行調研,再從這![]() 天中任取
天中任取![]() 天進行空氣顆粒物分析,求恰有
天進行空氣顆粒物分析,求恰有![]() 天空氣質量指數在
天空氣質量指數在![]() 上的概率.
上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() ,
,![]() 時,求滿足
時,求滿足![]() 的
的![]() 的值;
的值;
(2)若函數![]() 是定義在
是定義在![]() 上的奇函數.
上的奇函數.
①存在![]() ,使得不等式
,使得不等式![]() 有解,求實數
有解,求實數![]() 的取值范圍;
的取值范圍;
②若函數![]() 滿足
滿足![]() ,若對任意
,若對任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com