
已知![]() ,點
,點![]() 滿足
滿足![]() ,記點
,記點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求軌跡![]() 的方程;(Ⅱ)若直線
的方程;(Ⅱ)若直線![]() 過點
過點![]() 且與軌跡
且與軌跡![]() 交于
交于![]() 、
、![]() 兩點. (i)設(shè)點
兩點. (i)設(shè)點![]() ,問:是否存在實數(shù)
,問:是否存在實數(shù)![]() ,使得直線
,使得直線![]() 繞點
繞點![]() 無論怎樣轉(zhuǎn)動,都有
無論怎樣轉(zhuǎn)動,都有![]() 成立?若存在,求出實數(shù)
成立?若存在,求出實數(shù)![]() 的值;若不存在,請說明理由.(ii)過
的值;若不存在,請說明理由.(ii)過![]() 、
、![]() 作直線
作直線![]() 的垂線
的垂線![]() 、
、![]() ,垂足分別為
,垂足分別為![]() 、
、![]() ,記
,記
![]() ,求
,求![]() 的取值范圍.
的取值范圍.
(Ⅰ)![]()
(Ⅰ)由![]()
![]() 知,點
知,點![]() 的軌跡
的軌跡![]() 是以
是以![]() 、
、![]() 為焦點的雙曲線右支,由
為焦點的雙曲線右支,由![]() ,∴
,∴![]() ,故軌跡E的方程為
,故軌跡E的方程為![]() …………3分
…………3分
(Ⅱ)當(dāng)直線l的斜率存在時,設(shè)直線l方程為![]() ,與雙曲線方程聯(lián)立消
,與雙曲線方程聯(lián)立消![]() 得
得![]() ,設(shè)
,設(shè)![]() 、
、![]() ,
,
∴ , 解得
, 解得![]() ……………5分
……………5分
|

![]() ……………………7分
……………………7分
假設(shè)存在實數(shù)![]() ,使得
,使得![]() ,
,
故得![]() 對任意的
對任意的![]() 恒成立,
恒成立,
∴ ,解得
,解得![]() ∴當(dāng)
∴當(dāng)![]() 時,
時,![]() .
.
當(dāng)直線l的斜率不存在時,由![]() 及
及![]() 知結(jié)論也成立,
知結(jié)論也成立,
綜上,存在![]() ,使得
,使得![]() . …………………………………………8分
. …………………………………………8分
(ii)∵![]() ,∴直線
,∴直線![]() 是雙曲線的右準線,…………………………9分
是雙曲線的右準線,…………………………9分
由雙曲線定義得:![]() ,
,![]() ,
,
方法一:∴

![]() …………………………………………10分
…………………………………………10分
∵![]() ,∴
,∴![]() ,∴
,∴![]() ………………………………………11分
………………………………………11分
注意到直線的斜率不存在時,![]() ,綜上,
,綜上, …………………12分
…………………12分
|
與雙曲線右支有二個交點,∴![]() ,過
,過![]()
作![]() ,垂足為
,垂足為![]() ,則
,則![]() ,
,
∴![]()
 …(10分)
…(10分)
由![]() ,得
,得![]() 故:
故: …(12分)
…(12分)


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年廣西省高三第二次模擬考試理科數(shù)學(xué)試卷 題型:解答題
已知 ,
, ,點
,點 滿足
滿足 ,記點
,記點 的軌跡為
的軌跡為 ,過點
,過點 作直線
作直線 與軌跡
與軌跡 交于
交于 兩點,過
兩點,過 作直線
作直線 的垂線
的垂線 、
、 ,垂足分別為
,垂足分別為 ,記
,記 。
。
(1)求軌跡 的方程;
的方程;
(2)設(shè)點 ,求證:當(dāng)
,求證:當(dāng) 取最小值時,
取最小值時, 的面積為
的面積為 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011年遼寧省錦州市高二第一學(xué)期末理科數(shù)學(xué)卷 題型:解答題
(本小題滿分12分)
已知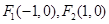 ,點
,點 滿足
滿足 ,記點
,記點 的軌跡為
的軌跡為 .
.
(Ⅰ)求軌跡 的方程;
的方程;
(Ⅱ)過點F2(1,0)作直線l與軌跡 交于不同的兩點A、B,設(shè)
交于不同的兩點A、B,設(shè) ,若
,若 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年上海市奉賢區(qū)高三第一學(xué)期調(diào)研測試數(shù)學(xué)文理合卷 題型:解答題
(文)已知 ,點
,點 滿足
滿足 ,記點
,記點 的軌跡為E,
的軌跡為E,
(1)、求軌跡E的方程;(5分)
(2)、如果過點Q(0,m)且方向向量為 =(1,1) 的直線l與點P的軌跡交于A,B兩點,當(dāng)
=(1,1) 的直線l與點P的軌跡交于A,B兩點,當(dāng) 時,求
時,求 AOB的面積。(9分)
AOB的面積。(9分)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分12分)
已知![]() ,點
,點![]() 滿足
滿足![]() ,記點
,記點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求軌跡![]() 的方程;
的方程;
(Ⅱ)過點F2(1,0)作直線l與軌跡![]() 交于不同的兩點A、B,設(shè)
交于不同的兩點A、B,設(shè)![]() ,若
,若![]() 的取值范圍。
的取值范圍。
|

|
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com