
【題目】“雙十一”期間,某淘寶店主對其商品的上架時間![]() (分鐘)和銷售量
(分鐘)和銷售量![]() (件)的關系作了統計,得到如下數據:
(件)的關系作了統計,得到如下數據:

經計算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)該店主通過作散點圖,發現上架時間與銷售量線性相關,請你幫助店主求出上架時間與銷售量的線性回歸方程(保留三位小數),并預測商品上架1000分鐘時的銷售量;
(2)從這11組數據![]() 中任選2組,設
中任選2組,設![]() 且
且![]() 的數據組數為
的數據組數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
附:線性回歸方程公式: 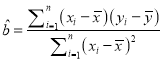 ,
, ![]()
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設公差大于0的等差數列{an}的前n項和為Sn,已知S3=15,且a1,a4,a13成等比數列,記數列 的前n項和為Tn.
的前n項和為Tn.
(Ⅰ)求Tn;
(Ⅱ)若對于任意的n∈N*,tTn<an+11恒成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解某校九年級1 600名學生的體能情況,隨機抽查了部分學生,測試1分鐘仰臥起坐的成績(次數),將數據整理后繪制成如圖所示的頻率分布直方圖,根據直方圖的數據,下列結論錯誤的是( )
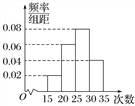
A. 該校九年級學生1分鐘仰臥起坐的次數的中位數為26.25
B. 該校九年級學生1分鐘仰臥起坐的次數的眾數為27.5
C. 該校九年級學生1分鐘仰臥起坐的次數超過30次的約有320人
D. 該校九年級學生1分鐘仰臥起坐的次數少于20次的約有32人
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“扶貧幫困”是中華民族的傳統美德,某校為幫扶困難同學,采用如下方式進行一次募捐:在不透明的箱子中放入大小均相同的白球七個,紅球三個,每位獻愛心的參與者投幣20元有一次摸獎機會,一次性從箱子中摸球三個(摸完球后將球放回),若有一個紅球,獎金10元,兩個紅球獎金20元,三個全是紅球獎金100元.
(1)求獻愛心參與者中將的概率;
(2)若該次募捐900位獻愛心參與者,求此次募捐所得善款的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,
, ![]() 、
、![]() 為橢圓的左右頂點,焦點到短軸端點的距離為2,
為橢圓的左右頂點,焦點到短軸端點的距離為2, ![]() 、
、![]() 為橢圓
為橢圓![]() 上異于
上異于![]() 、
、![]() 的兩點,且直線
的兩點,且直線![]() 的斜率等于直線
的斜率等于直線![]() 斜率的2倍.
斜率的2倍.

(Ⅰ)求證:直線![]() 與直線
與直線![]() 的斜率乘積為定值;
的斜率乘積為定值;
(Ⅱ)求三角形![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠引進一條先進生產線生產某種化工產品,其生產的總成本![]() (萬元)與年產量
(萬元)與年產量![]() (噸)之間的函數關系式可以近似的表示為
(噸)之間的函數關系式可以近似的表示為![]() ,已知此生產線年產量最大為
,已知此生產線年產量最大為![]() 噸.
噸.
(1)求年產量為多少噸時,生產每噸產品的平均成本最低,并求最低成本;
(2)若每噸產品平均出廠價為40萬元,那么當年產量為多少噸時,可以獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足an=2+2cos2![]() ,n∈N*,等差數列{bn}滿足a1=2b1,a2=b2.
,n∈N*,等差數列{bn}滿足a1=2b1,a2=b2.
(1)求bn;
(2)記cn=a2n-1b2n-1+a2nb2n,求cn;
(3)求數列{anbn}前2n項和S2n.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為F1(-c,0),F2(c,0),直線
的左、右焦點分別為F1(-c,0),F2(c,0),直線![]() 交橢圓E于A,B兩點,△ABF1的周長為16,△AF1F2的周長為12.
交橢圓E于A,B兩點,△ABF1的周長為16,△AF1F2的周長為12.
(1)求橢圓E的標準方程與離心率;
(2)若直線l與橢圓E交于C,D兩點,且P(2,2)是線段CD的中點,求直線l的一般方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com