
【題目】已知函數(shù)![]() , 則: (1)曲線
, 則: (1)曲線![]() 的斜率為
的斜率為![]() 的切線方程為__________;
的切線方程為__________;
(2)設![]() ,記
,記![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() .當
.當![]() 最小時,
最小時,![]() 的值為__________.
的值為__________.
 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,△PAD為正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E為棱PB的中點
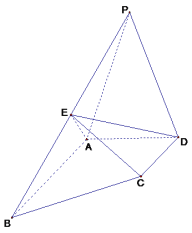
(1)求證:平面PAB⊥平面CDE;
(2)若AD=CD=2,求點P到平面ADE的距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列有關命題的說法正確的是( )
A.若“![]() ”為假命題,則“
”為假命題,則“![]() ”為假命題
”為假命題
B.“![]() ”是“
”是“![]() ”的必要不充分條件
”的必要不充分條件
C.命題“若![]() ,則
,則![]() ”的逆否命題為真命題
”的逆否命題為真命題
D.命題“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對于集合![]() ,定義函數(shù)
,定義函數(shù)![]() 對于兩個集合
對于兩個集合![]() ,定義集合
,定義集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)寫出![]() 和
和![]() 的值,并用列舉法寫出集合
的值,并用列舉法寫出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的個數(shù),求
所含元素的個數(shù),求![]() 的最小值;
的最小值;
(Ⅲ)有多少個集合對![]() ,滿足
,滿足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且2ccosB=2a+b.
(1)求角C的大小;
(2)若△ABC的面積等于![]() ,求ab的最小值.
,求ab的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 為等邊三角形,
為等邊三角形,![]() 為
為![]() 的中點.
的中點.
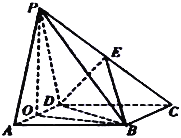
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ,并求四面體
,并求四面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知不等式|x+1|>|2﹣x|+1的解集為M,且a,b,c∈M.
(1)比較|a﹣b|與|1﹣ab|的大小,并說明理由;
(2)若![]() ,求a2+b2+c2的最小值.
,求a2+b2+c2的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】分形幾何學是一門以不規(guī)則幾何形態(tài)為研究對象的幾何學.分形的外表結構極為復雜,但其內部卻是有規(guī)律可尋的.一個數(shù)學意義上分形的生成是基于一個不斷迭代的方程式,即一種基于遞歸的反饋系統(tǒng).下面我們用分形的方法來得到一系列圖形,如圖1,線段![]() 的長度為
的長度為![]() ,在線段
,在線段![]() 上取兩個點
上取兩個點![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 為一邊在線段
為一邊在線段![]() 的上方做一個正六邊形,然后去掉線段
的上方做一個正六邊形,然后去掉線段![]() ,得到圖2中的圖形;對圖2中的最上方的線段
,得到圖2中的圖形;對圖2中的最上方的線段![]() 作相同的操作,得到圖3中的圖形;依此類推,我們就得到了以下一系列圖形:
作相同的操作,得到圖3中的圖形;依此類推,我們就得到了以下一系列圖形:
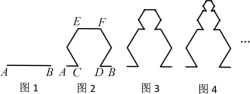
記第![]() 個圖形(圖1為第1個圖形)中的所有線段長的和為
個圖形(圖1為第1個圖形)中的所有線段長的和為![]() ,則(1)
,則(1)![]() ______;(2)如果對
______;(2)如果對![]() ,
,![]() 恒成立,那么線段
恒成立,那么線段![]() 的長度
的長度![]() 的取值范圍是_______.
的取值范圍是_______.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com