
【題目】函數f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的圖象與x軸相鄰兩個交點間的距離為
)的圖象與x軸相鄰兩個交點間的距離為 ![]() ,且圖象上一個最低點為M(
,且圖象上一個最低點為M( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的單調遞增區間;
(Ⅲ)當x∈[ ![]() ,
, ![]() ]時,求f(x)的值域.
]時,求f(x)的值域.
【答案】解:解:(Ⅰ)由圖象與x軸相鄰兩個交點間的距離為 ![]() ,
, ![]() =
= ![]() =
= ![]() ,∴ω=2, 再根據圖象上一個最低點為M(
,∴ω=2, 再根據圖象上一個最低點為M( ![]() ,﹣2),可得A=2,2×
,﹣2),可得A=2,2× ![]() +φ=
+φ= ![]() ,φ=
,φ= ![]() ,
,
∴f(x)=2sin(2x+ ![]() ).
).
(Ⅱ)令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z;
,k∈Z;
(Ⅲ)當x∈[ ![]() ,
, ![]() ]時,
]時, ![]() ≤2x+
≤2x+ ![]() ≤
≤ ![]() ,∴sin(2x+
,∴sin(2x+ ![]() )∈[﹣1,2],故函數的值域為[﹣1,2].
)∈[﹣1,2],故函數的值域為[﹣1,2].
【解析】(Ⅰ)由周期求得ω,由最低點的坐標結合五點法作圖求得A及φ的值,可得函數f(x)的解析式.(Ⅱ)由條件利用正弦函數的單調性,求得f(x)的單調遞增區間.(Ⅲ)當x∈[ ![]() ,
, ![]() ],利用正弦函數的定義域和值域,求得f(x)的值域.
],利用正弦函數的定義域和值域,求得f(x)的值域.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(x+1),g(x)=loga(4﹣2x),a>0且a≠1.
(1)求函數y=f(x)﹣g(x)的定義域;
(2)求使不等式f(x)>g(x)成立的實數x的取值范圍;
(3)求函數y=2f(x)﹣g(x)﹣f(1)的零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,集合A={x|1<x<4},B={x|x≤3m﹣4或x≥8+m}(m<6)
(1)若m=2,求A∩(UB)
(2)若A∩(UB)=,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型超市擬對店慶當天購物滿![]() 元的顧客進行回饋獎勵.規定:顧客轉動十二等分且質地均勻的圓形轉盤(如圖),待轉盤停止轉動時,若指針指向扇形區域,則顧客可領取此區域對應面額(單位:元)的超市代金券.假設轉盤每次轉動的結果互不影響.
元的顧客進行回饋獎勵.規定:顧客轉動十二等分且質地均勻的圓形轉盤(如圖),待轉盤停止轉動時,若指針指向扇形區域,則顧客可領取此區域對應面額(單位:元)的超市代金券.假設轉盤每次轉動的結果互不影響.
(Ⅰ)若![]() ,求顧客轉動一次轉盤獲得
,求顧客轉動一次轉盤獲得![]() 元代金券的概率;
元代金券的概率;
(Ⅱ)某顧客可以連續轉動兩次轉盤并獲得相應獎勵,當![]() 時,求該顧客第一次獲得代金券的面額不低于第二次獲得代金券的面額的概率;
時,求該顧客第一次獲得代金券的面額不低于第二次獲得代金券的面額的概率;
(Ⅲ)記顧客每次轉動轉盤獲得代金券的面額為![]() ,當
,當![]() 取何值時,
取何值時, ![]() 的方差最小?
的方差最小?
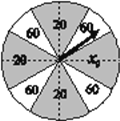
(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列![]() 中,
中, ![]() 分別是下表中第
分別是下表中第![]() 行中的某一個數,且
行中的某一個數,且![]() 中任何兩個數不在下表的同一列中.
中任何兩個數不在下表的同一列中.
第 | 第 | 第 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數列
,求數列![]() 的前
的前![]() 項和.
項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業招聘中,依次進行A科、B科考試,當A科合格時,才可考B科,且兩科均有一次補考機會,兩科都合格方通過.甲參加招聘,已知他每次考A科合格的概率均為 ![]() ,每次考B科合格的概率均為
,每次考B科合格的概率均為 ![]() .假設他不放棄每次考試機會,且每次考試互不影響.
.假設他不放棄每次考試機會,且每次考試互不影響.
(1)求甲恰好3次考試通過的概率;
(2)記甲參加考試的次數為ξ,求ξ的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=8 cm,AB=10 cm,點P由C出發以每秒2 cm的速度沿線段CA向點A運動(不運動至A點),⊙O的圓心在BP上,且⊙O分別與AB、AC相切,當點P運動2 s時,⊙O的半徑是( )
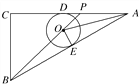
A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D. 2 cm
cm D. 2 cm
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com