【題目】已知向量
，函數(shù)
，若函數(shù)
的圖象與
軸的兩個相鄰交點的距離為
.
（1）求函數(shù)
的單調區(qū)間；
（2）若
時， 
，求
的值.
（3）若
，且
有且僅有一個實根，求實數(shù)
的值.
【答案】(1) 
；(2) 
；（3）
或
【解析】試題分析：（1）首先化簡
，利用函數(shù)
圖象與
軸的兩個相鄰交點的距離為
得到周期為
，由此求得
的值，即求得函數(shù)的表達式，由此求和函數(shù)的單調區(qū)間.（2）利用（1）的結論有
，即
，由此求得
，利用
展開后可求得
的值.（3）先根據(jù)
求得
.在同一直角坐標系中作出
兩個函數(shù)圖象，可知
或
.
試題解析：
(1)函數(shù)
， 
函數(shù)
圖象與
軸的兩個相鄰交點的距離為
， 
，解得
， 
，由
，得
，即
，所以函數(shù)
的單調增區(qū)間為
.
(2)由（1）得
，
， 
， 
.
（3）
， 
，且余弦函數(shù)在
上是減函數(shù)， 
，在同一直角坐標系中作出
兩個函數(shù)圖象，可知
或
.
期末100分闖關海淀考王系列答案
小學能力測試卷系列答案科目：高中數(shù)學 來源： 題型：
【題目】在研究色盲與性別的關系調查中，調查了男性480人，其中有38人患色盲，調查的520個女性中6人患色盲．
（Ⅰ）根據(jù)題中數(shù)據(jù)建立一個
的列聯(lián)表；
（Ⅱ）在犯錯誤的概率不超過0.001的前提下，能否認為“性別與患色盲有關系”？
附：參考公式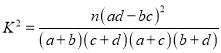
， 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
， 
.
（Ⅰ）若
是奇函數(shù)，且在區(qū)間
上是增函數(shù)，求
的值；
（Ⅱ）設
，若
在區(qū)間
內有兩個不同的零點
， 
，求
的取值范圍，并求
的值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】選修4-4：坐標系與參數(shù)方程
在直角坐標系
中，直線
的參數(shù)方程為
（
為參數(shù)）．在以原點
為極點，
軸的正半軸為極軸的極坐標系中，曲線
的極坐標方程為
．
（1）直接寫出直線
、曲線
的直角坐標方程；
（2）設曲線
上的點到直線
的距離為
，求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
,其中
，且函數(shù)
的最小正周期為
。
（1）若函數(shù)
在
處取到最小值
，求函數(shù)
的解析式；
（2）若將函數(shù)
圖象上所有點的橫坐標伸長到原來的
倍（縱坐標不變），再將向左平移
個單位，得到的函數(shù)圖象關于
軸對稱，求函數(shù)
的單調遞增區(qū)間。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】“真人秀”熱潮在我國愈演愈烈，為了了解學生是否喜歡某“真人秀”節(jié)目，在某中學隨機調查了110名學生，得到如下列聯(lián)表：
男 | 女 | 總計 | |
喜歡 | 40 | 20 | 60 |
不喜歡 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
由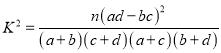
算得
.
附表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
參照附表，得到的正確結論是（ ）
A. 在犯錯誤的概率不超過
的前提下，認為“喜歡該節(jié)目與性別有關”
B. 在犯錯誤的概率不超過
的前提下，認為“喜歡該節(jié)目與性別無關”
C. 有
以上的把握認為“喜歡該節(jié)目與性別有關”
D. 有
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】隨機抽取了40輛汽車在經(jīng)過路段上某點是的車速（
），現(xiàn)將其分成六段：
，
后得到如圖所示的頻率分布直方圖.
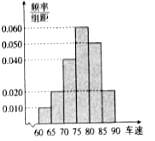
（I）現(xiàn)有某汽車途經(jīng)該點，則其速度低于80
的概率約是多少？
（II）根據(jù)頻率分布直方圖，抽取的40輛汽車經(jīng)過該點的平均速度是多少？
（III）在抽取的40輛汽車且速度在
（）內的汽車中任取2輛，求這2輛車車速都在
（）內的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
