
【題目】如圖,多面體![]() 是正三棱柱(底面是正三角形的直棱柱)
是正三棱柱(底面是正三角形的直棱柱)![]() 沿平面
沿平面![]() 切除一部分所得,其中平面
切除一部分所得,其中平面![]() 為原正三棱柱的底面,
為原正三棱柱的底面,![]() ,點(diǎn)D為
,點(diǎn)D為![]() 的中點(diǎn).
的中點(diǎn).
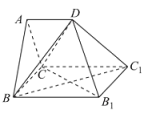
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)設(shè)![]() 與
與![]() 交于點(diǎn)E,連接
交于點(diǎn)E,連接![]() 、
、![]() ,由題意可得四邊形
,由題意可得四邊形![]() 是正方形,且
是正方形,且![]() ,再由點(diǎn)D為
,再由點(diǎn)D為![]() 的中點(diǎn),
的中點(diǎn),![]() 平行且等于
平行且等于![]() ,求得CD,同理求得
,求得CD,同理求得![]() ,得
,得![]() ,可得
,可得![]() ,由線面垂直的判定可得;
,由線面垂直的判定可得;
(2)取BC的中點(diǎn)O,連接AO,可得AO⊥BC,由正棱柱的性質(zhì)可得AO⊥平面![]() ,以O為坐標(biāo)原點(diǎn),向量
,以O為坐標(biāo)原點(diǎn),向量![]() 、
、![]() 、
、![]() 分別為x、y,z軸建立空間直角坐標(biāo)系,分別求出平面CBD與平面
分別為x、y,z軸建立空間直角坐標(biāo)系,分別求出平面CBD與平面![]() 的一個法向量,由兩法向量所成角的余弦值可得二面角
的一個法向量,由兩法向量所成角的余弦值可得二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(1)設(shè)![]() 與
與![]() 交于點(diǎn)E,連接
交于點(diǎn)E,連接![]() 、
、![]() .
.
∵多面體![]() 是正三棱柱沿平面
是正三棱柱沿平面![]() 切除部分所得,
切除部分所得,![]() ,
,
∴四邊形![]() 是正方形,且
是正方形,且![]() .
.
∵點(diǎn)D為![]() 的中點(diǎn),
的中點(diǎn),![]() 平行且等于
平行且等于![]() ,
,
∴![]() .
.
同理![]() ,
,
∴![]() .
.
∵E為![]() 的中點(diǎn),
的中點(diǎn),
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ;
;
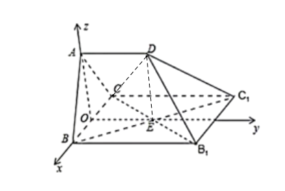
(2)取![]() 的中點(diǎn)O,連接
的中點(diǎn)O,連接![]() .
.
∵![]() 為正三角形,
為正三角形,![]() .
.
由正棱柱的性質(zhì)可得,平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
以點(diǎn)O為原點(diǎn),向量![]() 、
、![]() 、
、![]() 分別為x、y,z軸正方向建立如圖所示空間直角坐標(biāo)系
分別為x、y,z軸正方向建立如圖所示空間直角坐標(biāo)系![]() .
.
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
設(shè)平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則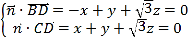 ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
由(1)可知,平面![]() 的一個法向量為
的一個法向量為![]() .
.
 ,
,
又∵二面角![]() 的平面角為銳角,
的平面角為銳角,
∴二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于數(shù)列![]() ,定義“
,定義“![]() 變換”:
變換”:![]() 將數(shù)列
將數(shù)列![]() 變換成數(shù)列
變換成數(shù)列![]() ,其中
,其中![]() ,且
,且![]() ,這種“
,這種“![]() 變換”記作
變換”記作![]() .繼續(xù)對數(shù)列
.繼續(xù)對數(shù)列![]() 進(jìn)行“
進(jìn)行“![]() 變換”,得到數(shù)列
變換”,得到數(shù)列![]() ,依此類推,當(dāng)?shù)玫降臄?shù)列各項均為
,依此類推,當(dāng)?shù)玫降臄?shù)列各項均為![]() 時變換結(jié)束.
時變換結(jié)束.
(1)試問![]() 和
和![]() 經(jīng)過不斷的“
經(jīng)過不斷的“![]() 變換”能否結(jié)束?若能,請依次寫出經(jīng)過“
變換”能否結(jié)束?若能,請依次寫出經(jīng)過“![]() 變換”得到的各數(shù)列;若不能,說明理由;
變換”得到的各數(shù)列;若不能,說明理由;
(2)求![]() 經(jīng)過有限次“
經(jīng)過有限次“![]() 變換”后能夠結(jié)束的充要條件;
變換”后能夠結(jié)束的充要條件;
(3)證明:![]() 一定能經(jīng)過有限次“
一定能經(jīng)過有限次“![]() 變換”后結(jié)束.
變換”后結(jié)束.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題中錯誤的是( )
A.若命題![]() 為真命題,命題
為真命題,命題![]() 為假命題,則命題“
為假命題,則命題“![]() ”為真命題
”為真命題
B.命題“若![]() ,則
,則![]() 或
或![]() ”為真命題
”為真命題
C.命題“若![]() ,則
,則![]() 或
或![]() ”的否命題為“若
”的否命題為“若![]() ,則
,則![]() 且
且![]() ”
”
D.命題![]() :
:![]() ,
,![]() ,則
,則![]() 為
為![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知F1,F2為橢圓E:![]() 的左、右焦點(diǎn),且|F1F2|=2
的左、右焦點(diǎn),且|F1F2|=2![]() ,點(diǎn)
,點(diǎn)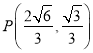 在E上.
在E上.
(1)求E的方程;
(2)直線l與以E的短軸為直徑的圓相切,l與E交于A,B兩點(diǎn),O為坐標(biāo)原點(diǎn),試判斷O與以AB為直徑的圓的位置關(guān)系,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 的參數(shù)方程為
的參數(shù)方程為![]() (其中
(其中![]() 為參數(shù)),以原點(diǎn)為極點(diǎn),
為參數(shù)),以原點(diǎn)為極點(diǎn),![]() 軸非負(fù)半軸為極軸建立極坐標(biāo)系,則曲線
軸非負(fù)半軸為極軸建立極坐標(biāo)系,則曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求圓![]() 的普通方程與
的普通方程與![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)點(diǎn)![]() 是曲線
是曲線![]() 上一點(diǎn),由
上一點(diǎn),由![]() 向圓
向圓![]() 引切線,切點(diǎn)分別為
引切線,切點(diǎn)分別為![]() ,求四邊形
,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某人某天的工作是駕車從![]() 地出發(fā),到
地出發(fā),到![]() 兩地辦事,最后返回
兩地辦事,最后返回![]() 地,
地,![]() ,三地之間各路段行駛時間及擁堵概率如下表
,三地之間各路段行駛時間及擁堵概率如下表
路段 | 正常行駛所用時間(小時) | 上午擁堵概率 | 下午擁堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到擁堵,則在該路段行駛時間需要延長1小時.
現(xiàn)有如下兩個方案:
方案甲:上午從![]() 地出發(fā)到
地出發(fā)到![]() 地辦事然后到達(dá)
地辦事然后到達(dá)![]() 地,下午從
地,下午從![]() 地辦事后返回
地辦事后返回![]() 地;
地;
方案乙:上午從![]() 地出發(fā)到
地出發(fā)到![]()
![]() 地出發(fā)到達(dá)
地出發(fā)到達(dá)![]() 地,辦完事后返回
地,辦完事后返回![]() 地.
地.
(1)若此人早上8點(diǎn)從![]() 地出發(fā),在各地辦事及午餐的累積時間為2小時,且采用方案甲,求他當(dāng)日18點(diǎn)或18點(diǎn)之前能返回
地出發(fā),在各地辦事及午餐的累積時間為2小時,且采用方案甲,求他當(dāng)日18點(diǎn)或18點(diǎn)之前能返回![]() 地的概率.
地的概率.
(2)甲乙兩個方案中,哪個方案有利于辦完事后更早返回![]() 地?請說明理由.
地?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某市管轄的海域內(nèi)有一圓形離岸小島,半徑為1公里,小島中心O到岸邊AM的最近距離OA為2公里.該市規(guī)劃開發(fā)小島為旅游景區(qū),擬在圓形小島區(qū)域邊界上某點(diǎn)B處新建一個浴場,在海岸上某點(diǎn)C處新建一家五星級酒店,在A處新建一個碼頭,且使得AB與AC滿足垂直且相等,為方便游客,再建一條跨海高速通道OC連接酒店和小島,設(shè)![]() .
.
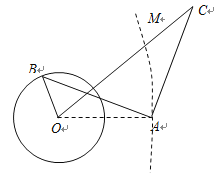
(1)設(shè)![]() ,試將
,試將![]() 表示成
表示成![]() 的函數(shù);
的函數(shù);
(2)若OC越長,景區(qū)的輻射功能越強(qiáng),問當(dāng)![]() 為何值時OC最長,并求出該最大值.
為何值時OC最長,并求出該最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com