
【題目】已知函數![]() ,
, ![]() .
.
(1)求函數![]() 在
在![]() 的最小值;
的最小值;
(2)若函數![]() 與
與![]() 的圖象恰有一個公共點,求實數
的圖象恰有一個公共點,求實數![]() 的值;
的值;
(3)若函數![]() 有兩個不同的極值點
有兩個不同的極值點![]() ,且
,且![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)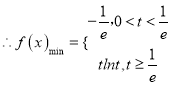 ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】試題分析:(Ⅰ)由![]() ,得極值點為
,得極值點為![]() ,分情況討論
,分情況討論![]() 及
及![]() 時,函數
時,函數![]() 的最小值;(Ⅱ)當函數
的最小值;(Ⅱ)當函數![]() 有兩個不同的極值點,即
有兩個不同的極值點,即![]() 有兩個不同的實根
有兩個不同的實根![]() ,問題等價于直線
,問題等價于直線![]() 與函數
與函數![]() 的圖象有兩個不同的交點,由
的圖象有兩個不同的交點,由![]() 單調性結合函數圖象可知當
單調性結合函數圖象可知當![]() 時,
時, ![]() 存在,且
存在,且![]() 的值隨著
的值隨著![]() 的增大而增大,而當
的增大而增大,而當![]() 時,由題意
時,由題意![]() ,
, ![]() 代入上述方程可得
代入上述方程可得![]() ,此時實數
,此時實數![]() 的取值范圍為
的取值范圍為![]() .
.
試題解析:(Ⅰ)由![]() ,可得
,可得![]() ,
,
![]() ①
①![]() 時,函數
時,函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
![]() 函數
函數![]() 在
在![]() 上的最小值為
上的最小值為![]() ,
,
②當![]() 時,
時,![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,
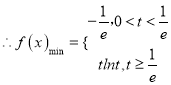 ;
;
(Ⅱ)![]() ,則
,則![]()
題意即為![]() 有兩個不同的實根
有兩個不同的實根![]() ,
,
即![]() 有兩個不同的實根
有兩個不同的實根![]() ,
,
等價于直線![]() 與函數
與函數![]() 的圖像有兩個不同的交點,
的圖像有兩個不同的交點,
![]() ,
, ![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
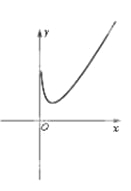
畫出函數圖像的大致形狀(如右圖),
由圖像知,當![]() 時,
時, ![]() 存在,且
存在,且![]() 的值隨著
的值隨著![]() 的增大
的增大
而增大,而當![]() 時,由題意
時,由題意![]() ,
,
兩式相減可得![]()
![]() 代入上述方程可得
代入上述方程可得![]() ,
,
此時![]() ,
,
所以,實數![]() 的取值范圍為
的取值范圍為![]() ;
;


科目:高中數學 來源: 題型:
【題目】如下莖葉圖記錄了某NBA籃球隊內兩大中鋒在六次訓練中搶得籃板球數記錄,由于教練一時疏忽,忘了記錄乙球員其中一次的數據,在圖中以X表示。
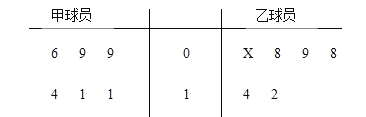
(1)如果乙球員搶得籃板球的平均數為10時,求X的值和乙球員搶得籃板球數的方差;
(2)如果您是該球隊的教練在正式比賽中您會派誰上場呢?并說明理由(用數據說明)。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() ,直線
,直線![]() 交橢圓
交橢圓![]() 于不同的兩點
于不同的兩點![]() ,設線段
,設線段![]() 的中點為
的中點為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)當![]() 的面積為
的面積為![]() (其中
(其中![]() 為坐標原點)且
為坐標原點)且![]() 時,試問:在坐標平面上是否存在兩個定點
時,試問:在坐標平面上是否存在兩個定點![]() ,使得當直線
,使得當直線![]() 運動時,
運動時,![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 的坐標和定值;若不存在,請說明理由.
的坐標和定值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于for x=a:b:c,下列說法正確的有( )
①當x=c時程序結束;②當x=c時,還要繼續執行一次;③當b>0時,x≥a時程序結束;④當b<0時,x<a時程序結束.
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,C.已知3cos(B-C)-1=6cosBcosC.
(1)求cosA;
(2)若a=3,△ABC的面積為![]() ,求邊b和c.
,求邊b和c.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王在年初用50萬元購買一輛大貨車,第一年因繳納各種費用需支出6萬元,從第二年起,每年都比上一年增加支出2萬元,假定該車每年的運輸收入均為25萬元.小王在該車運輸累計收入超過總支出后,考慮將大貨車作為二手車出售,若該車在第x年年底出售,其銷售價格為25-x萬元(國家規定大貨車的報廢年限為10年).
(1)大貨車運輸到第幾年年底,該車運輸累計收入超過總支出?
(2)在第幾年年底將大貨車出售,能使小王獲得的年平均利潤最大(利潤=累計收入+銷售收入-總支出)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com