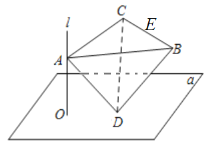
【題目】如圖，直線
平面
，垂足為
，正四面體
的棱長為2，
，
分別是直線
和平面上的動點，且
，則下列判斷：①點到棱
中點
的距離的最大值為
；②正四面體在平面上的射影面積的最大值為
．其中正確的說法是（ ）．
A.①②都正確B.①②都錯誤C.①正確，②錯誤D.①錯誤，②正確
【答案】C
【解析】
由題意，點
在以
為直徑的球面上的點，所以點到棱
中點
的距離的最大值為點到球心的距離再加上球的半徑，可判斷①，當當
與重合時，求出正四面體
在在平面
上的射影面積，可判斷②.
由題意，點在以為直徑的球面上的點.
點到棱中點的距離，即以為直徑的球面上的點到棱中點的距離.
所以點到棱中點的距離的最大值為點到球心的距離再加上球的半徑.
設的中點為
，則為以為直徑的球的球心，半徑為
所以
所以點到棱中點的距離的最大值為
，故正確①.
由直線
平面，且
，則
平面.
在正四面體中，
,又，所以
平面
所以在平面上的射影
與平行且相等.
當與重合時，正四面體在在平面上的射影為對角線為2的正方形.
此時射影的面積為2，所以②不正確.
故選：C
科目：高中數學 來源： 題型：
【題目】如圖是國家統計局于2020年1月9日發布的2018年12月到2019年12月全國居民消費價格的漲跌幅情況折線圖.（注：同比是指本期與同期作對比；環比是指本期與上期作對比.如：2019年2月與2018年2月相比較稱同比，2019年2月與2019年1月相比較稱環比）根據該折線圖，下列結論錯誤的是（ ）
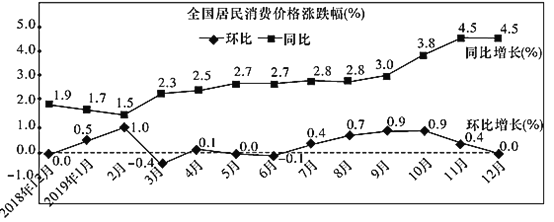
A.2019年12月份，全國居民消費價格環比持平
B.2018年12月至2019年12月全國居民消費價格環比均上漲
C.2018年12月至2019年12月全國居民消費價格同比均上漲
D.2018年11月的全國居民消費價格高于2017年12月的全國居民消費價格
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校開設了射擊選修課，規定向
、
兩個靶進行射擊：先向靶射擊一次，命中得1分，沒有命中得0分，向靶連續射擊兩次，每命中一次得2分，沒命中得0分；小明同學經訓練可知：向靶射擊，命中的概率為
，向靶射擊，命中的概率為
，假設小明同學每次射擊的結果相互獨立.現對小明同學進行以上三次射擊的考核.
（1）求小明同學恰好命中一次的概率；
（2）求小明同學獲得總分
的分布列及數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，直線l的參數方程為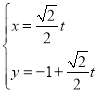
（t為參數），以原點O為極點，x正半軸為極軸建立極坐標系，曲線的極坐標方程為
.
（1）求直線l的普通方程和曲線C的直角坐標方程；
（2）設P（0，-1），直線l與C的交點為M，N，線段MN的中點為Q，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正項數列
中，
，點
在拋物線
上.數列
中，點
在經過點
，以
為方向向量的直線
上.
（1）求數列，的通項公式；
（2）若
，問是否存在
，使得
成立？若存在，求出
的值；若不存在，說明理由；
（3）對任意的正整數
，不等式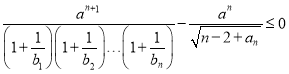
成立，求正數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
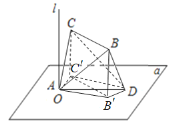
【題目】將邊長為5的菱形ABCD沿對角線AC折起，頂點B移動至
處，在以點B'，A，C，為頂點的四面體AB'CD中，棱AC、B'D的中點分別為E、F，若AC＝6，且四面體AB'CD的外接球球心落在四面體內部，則線段EF長度的取值范圍為（ ）
A.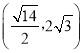
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動圓與
軸相切于點
，過點
，
分別作動圓異于軸的兩切線，設兩切線相交于
，點的軌跡為曲線
.
（1）求曲線的軌跡方程；
（2）過
的直線
與曲線相交于不同兩點
，若曲線上存在點
，使得
成立，求實數
的范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
