
���}Ŀ����D���������F![]() �У�����
�У�����![]() �����Σ�
�����Σ�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �քe��
�քe��![]() ��
��![]() �����c(di��n).
�����c(di��n).
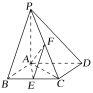
(1)���C��![]() ��
��
(2)�O(sh��)![]() �龀��
�龀��![]() �ϵĄ�(d��ng)�c(di��n)��������
�ϵĄ�(d��ng)�c(di��n)��������![]() �L(zh��ng)����Сֵ��
�L(zh��ng)����Сֵ��![]() ��������
��������![]() ������ֵ.
������ֵ.
���𰸡���1���C��Ҋ��������2��![]() .
.
��������
��1������(j��)���洹ֱ���ж��������õ�![]() ƽ��
ƽ��![]() ���M(j��n)�����Ƴ��Y(ji��)Փ������
���M(j��n)�����Ƴ��Y(ji��)Փ������
��2��![]() �龀��
�龀��![]() �ϵĄ�(d��ng)�c(di��n)���B��
�ϵĄ�(d��ng)�c(di��n)���B��![]() ��
��![]() ������(j��)�}��õ�
������(j��)�}��õ�![]() ���ɣ�1����
���ɣ�1����![]() ��
��![]() ��
��![]() �Ƀɴ�ֱ����
�Ƀɴ�ֱ����![]() ������(bi��o)ԭ�c(di��n)���������gֱ������(bi��o)ϵ���քe���ƽ��
������(bi��o)ԭ�c(di��n)���������gֱ������(bi��o)ϵ���քe���ƽ��![]() �cƽ��
�cƽ��![]() �ķ��������������A�ǹ�ʽ�����ɵó��Y(ji��)��.
�ķ��������������A�ǹ�ʽ�����ɵó��Y(ji��)��.
(1)����߅��![]() �����Σ�
������![]() ��
��
��![]() ����������.
����������.
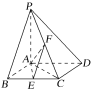
��![]() ��
��![]() �����c(di��n)����
�����c(di��n)����![]() .
.
��![]() ����
����![]() .
.
��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
��![]() .
.
��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ����
����![]() ��
��
��![]() ƽ��
ƽ��![]() ��
��
��![]() ƽ��
ƽ��![]() ����
����![]() ��
��
(2)��D��![]() �龀��
�龀��![]() �ϵĄ�(d��ng)�c(di��n)���B��
�ϵĄ�(d��ng)�c(di��n)���B��![]() ��
��![]() .
.
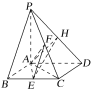
��(d��ng)����![]() ���L(zh��ng)���r(sh��)��
���L(zh��ng)���r(sh��)��![]() .
.
��(1)֪![]() ����
����![]() ��
��
��![]() ƽ��
ƽ��![]() .
.
��![]() ƽ��
ƽ��![]() ����
����![]() .
.
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��![]() ����֪
����֪![]() ����
����![]() .
.
����![]() �У��ɵ�
�У��ɵ�![]() .
.
��(1)��֪![]() ��
��![]() ��
��![]() �Ƀɴ�ֱ����
�Ƀɴ�ֱ����![]() ������(bi��o)ԭ�c(di��n)��������D��ʾ�Ŀ��gֱ������(bi��o)ϵ.��
������(bi��o)ԭ�c(di��n)��������D��ʾ�Ŀ��gֱ������(bi��o)ϵ.��![]() ��
��![]() �քe��
�քe��![]() ��
��![]() �����c(di��n)���ɵ�
�����c(di��n)���ɵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��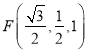 ��
��
����![]() ��
��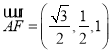 .
.
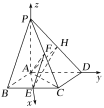
�O(sh��)ƽ��![]() �ķ�������
�ķ�������![]() ��
��
�t �����
�����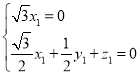 ��
��
ȡ![]() ����
����![]() .
.
��?y��n)?/span>![]() ��
��![]() ��
��![]() ��
��
����![]() ƽ��
ƽ��![]() ��
��
��![]() ��ƽ��
��ƽ��![]() ��һ��(g��)������.
��һ��(g��)������.
��![]() ��
��
����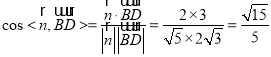 .
.
�ɈD��֪�����![]() ���J�ǣ����������ǵ�����ֵ��
���J�ǣ����������ǵ�����ֵ��![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
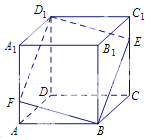
���}Ŀ����D��ʾ���������w![]() �У��c(di��n)
���c(di��n)![]() ����
����![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)��ƽ��
�ϵ�һ��(g��)��(d��ng)�c(di��n)��ƽ��![]() ����
����![]() ���c(di��n)
���c(di��n)![]() ���o���������}��
���o���������}��
�ٴ����c(di��n)![]() ��ʹ��
��ʹ��![]() //ƽ��
//ƽ��![]() ��
��
����(du��)��������c(di��n)![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��
�������c(di��n)![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ��
��
�܌�(du��)��������c(di��n)![]() �������F
�������F![]() ���w�e����׃.
���w�e����׃.
�������_���}����̖(h��o)��______���������������_���}����̖(h��o)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��2020�꺮��������ĺ��٣���?y��n)鿹������ȫ�w�W(xu��)��ֻ���ڼ��M(j��n)�оW(w��ng)���ھ��W(xu��)��(x��)�������о��W(xu��)���ھW(w��ng)�όW(xu��)��(x��)����r��ij�W(xu��)У�ھW(w��ng)���S�C(j��)��ȡ120���W(xu��)����(du��)���Ͻ����M(j��n)���{(di��o)�飬���������cŮ�����˔�(sh��)֮�Ȟ�11��13����������30�ˌ�(du��)�ھ��Ͻ����M�⣬Ů������15����ʾ��(du��)���Ͻ������M��.
��1�����![]() ��(li��n)�������ش��ܷ���99%�İ����J(r��n)�錦(du��)�����Ͻ����Ƿ�M���c�Ԅe���P(gu��n)����
��(li��n)�������ش��ܷ���99%�İ����J(r��n)�錦(du��)�����Ͻ����Ƿ�M���c�Ԅe���P(gu��n)����
�M�� | ���M�� | ��Ӌ(j��) | |
���� | 30 | ||
�� | 15 | ||
��Ӌ(j��) | 120 |
��2���ı��{(di��o)��Č�(du��)���Ͻ����M��ČW(xu��)���У����÷ӳ�ӳ�ȡ8���W(xu��)��������8���W(xu��)���г�ȡ3���W(xu��)���������όW(xu��)��(x��)�Ľ�(j��ng)�(y��n)��B�����г�ȡ�����Ă�(g��)��(sh��)��![]() �����
�����![]() �ķֲ��м�����ֵ.
�ķֲ��м�����ֵ.
������ʽ������
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() ����(j��ng)�^(gu��)
����(j��ng)�^(gu��)![]() �c
�c ���c(di��n).
���c(di��n).

��1����E�A![]() �ķ��̣�
�ķ��̣�
��2���^(gu��)ԭ�c(di��n)��ֱ��![]() �c�E�A
�c�E�A![]() ����
����![]() ���c(di��n)���E�A
���c(di��n)���E�A![]() ��һ�c(di��n)
��һ�c(di��n)![]() �M��
�M��![]() �����C��
�����C�� ![]() �鶨ֵ.
�鶨ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D����֪���c(di��n)��x�S�ϵęE�A![]() ��һ��(g��)��(n��i)���Ax2��y2=
��һ��(g��)��(n��i)���Ax2��y2=![]() ��ԓ�A�Ĵ�ֱ��x�S���о����E�A���c(di��n)M��N����
��ԓ�A�Ĵ�ֱ��x�S���о����E�A���c(di��n)M��N����![]() (O��ԭ�c(di��n)).
(O��ԭ�c(di��n)).

��1����b��ֵ��
��2���O(sh��)��(n��i)���A�������о�l���E�A���c(di��n)A��B.���C��![]() ������|AB|��ȡֵ����.
������|AB|��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ��
��![]() ���^(gu��)
���^(gu��)![]() ���c
���c![]() �S��ֱ��ֱ�����E�A
�S��ֱ��ֱ�����E�A![]() �͈A
�͈A![]() �صõ����L(zh��ng)�քe��2��
�صõ����L(zh��ng)�քe��2��![]() .
.
��1����![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����֪?ji��ng)�ֱ��![]() �c���タ
�c���タ![]() ��
��![]() ���У����c(di��n)����ԭ�c(di��n)������
���У����c(di��n)����ԭ�c(di��n)������![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)����(w��n)���E�A
���c(di��n)����(w��n)���E�A![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ��
��ʹ��![]() ������������M��l��������
������������M��l��������![]() �c(di��n)������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
�c(di��n)������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�������f(shu��)�������_���ǣ� ��
A.��(du��)���о������P(gu��n)�P(gu��n)ϵ��׃��![]() ��һ�M�^�y(c��)��(sh��)��(j��)
��һ�M�^�y(c��)��(sh��)��(j��)![]() ���侀�Իؚw������
���侀�Իؚw������![]() ����
����![]() ���t��(sh��)��(sh��)
���t��(sh��)��(sh��)![]() ��ֵ��
��ֵ��![]()
B.���B(t��i)�ֲ�![]() �څ^(q��)�g
�څ^(q��)�g![]() ��
��![]() ��ȡֵ�ĸ������
��ȡֵ�ĸ������
C.��ɂ�(g��)�S�C(j��)׃���ľ������P(gu��n)��Խ��(qi��ng)���t���P(gu��n)ϵ��(sh��)![]() ��ֵԽ�ӽ���1
��ֵԽ�ӽ���1
D.��һ�M��(sh��)��(j��)![]() ��ƽ����(sh��)��2���t�@�M��(sh��)��(j��)�ı���(sh��)����λ��(sh��)����2
��ƽ����(sh��)��2���t�@�M��(sh��)��(j��)�ı���(sh��)����λ��(sh��)����2
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
(1)��![]() ��������
��������![]() ���c(di��n)
���c(di��n)![]() ̎���о����̣�
̎���о����̣�
(2)��(du��)�����![]() ��
��![]() ������
������![]() ��������(sh��)
��������(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() ��
��![]() �ǙE�A���p�����Ĺ������c(di��n)��
�ǙE�A���p�����Ĺ������c(di��n)��![]() ��������һ��(g��)�����c(di��n)����
��������һ��(g��)�����c(di��n)����![]() ���t�E�A���p�������x���ʵĵ���(sh��)֮�͵����ֵ��___.
���t�E�A���p�������x���ʵĵ���(sh��)֮�͵����ֵ��___.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com