
【題目】已知函數![]() ,
,
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)對任意的![]() ,
,![]() ,恒有
,恒有![]() ,求正數
,求正數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)求出函數的導數,進而求得![]() ,由點斜式直接寫出直線方程.
,由點斜式直接寫出直線方程.
(2)求出2a+1的范圍,可得f(x)在[1,2]遞減,由題意可得原不等式即為![]() 對任意的a∈[
對任意的a∈[![]() ,
,![]() ],x1,x2∈[1,2]恒成立,令g(x)=f(x)
],x1,x2∈[1,2]恒成立,令g(x)=f(x)![]() ,即有g(x1)<g(x2),即為g(x)在[1,2]遞增,求出g(x)的導數,令導數大于等于0,再由一次函數的單調性可得只需以
,即有g(x1)<g(x2),即為g(x)在[1,2]遞增,求出g(x)的導數,令導數大于等于0,再由一次函數的單調性可得只需以![]() .
.
即x3﹣7x2+6x+λ≥0對x∈[1,2]恒成立,令h(x)=x3﹣7x2+6x+λ,求出導數,求得單調區間和最小值,解不等式即可得到所求范圍.
(1)![]() ,所以
,所以![]() ,又f(3)=
,又f(3)=![]() ,
,
所以由點斜式方程可得切線方程為![]() .
.
(2)![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上為減函數,
上為減函數,
不妨設![]() 則,
則,![]() 等價于
等價于![]()
所以![]() ,在
,在![]() ,
,![]() 上恒成立。
上恒成立。
令![]() ,則
,則![]() 在
在![]() 上為增函數,所以
上為增函數,所以![]() 在
在![]()
![]() 上恒成立.
上恒成立.
而![]() 化簡得
化簡得![]() ,
,
所以![]() ,其中
,其中![]()
因為![]() ,所以
,所以![]()
所以只需![]() ,即x3﹣7x2+6x+λ≥0對x∈[1,2]恒成立,
,即x3﹣7x2+6x+λ≥0對x∈[1,2]恒成立,
令h(x)=x3﹣7x2+6x+λ,h′(x)=3x2﹣14x+6≤0在1≤x≤2恒成立,
則有h(x)在[1,2]遞減,可得h(2)取得最小值,且為﹣8+λ≥0,
解得λ≥8.
所以![]() .
.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源: 題型:
【題目】某研究機構對高三學生的記憶力x和判斷力y進行統計分析,得下表數據.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)請根據上表提供的數據,求出y關于x的線性回歸方程![]() ;
;
(2)判斷該高三學生的記憶力x和判斷力是正相關還是負相關;并預測判斷力為4的同學的記憶力.
(參考公式: )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的函數
上的函數![]() 滿足
滿足![]() ,
,![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)求函數![]() 的單調區間;
的單調區間;
(3)如果![]() 、
、![]() 、
、![]() 滿足
滿足![]() ,那么稱
,那么稱![]() 比
比![]() 更靠近
更靠近![]() .當
.當![]() 且
且![]() 時,試比較
時,試比較![]() 和
和![]() 哪個更靠近
哪個更靠近![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=sinx的圖象向右平移![]() 個單位,橫坐標縮小至原來的
個單位,橫坐標縮小至原來的![]() 倍(縱坐標不變)得到函數y=g(x)的圖象.
倍(縱坐標不變)得到函數y=g(x)的圖象.
(1)求函數g(x)的解析式;
(2)若關于x的方程2g(x)-m=0在x∈[0,![]() ]時有兩個不同解,求m的取值范圍.
]時有兩個不同解,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列1,1,3,3,![]() ,
,![]() ,…,
,…,![]() ,
,![]() 是由兩個1,兩個3,兩個
是由兩個1,兩個3,兩個![]() ,…,兩個
,…,兩個![]() 按從小到大順序排列,數列各項的和記為
按從小到大順序排列,數列各項的和記為![]() ,對于給定的自然數
,對于給定的自然數![]() ,若能從數列中選取一些不同位置的項,使得這些項之和恰等于
,若能從數列中選取一些不同位置的項,使得這些項之和恰等于![]() ,便稱為一種選項方案,和數為
,便稱為一種選項方案,和數為![]() 的所有選項方案的種數記為
的所有選項方案的種數記為![]() .試求:
.試求:
![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究某學科成績是否與學生性別有關,采用分層抽樣的方法,從高三年級抽取了30名男生和20名女生的該學科成績,得到如下所示男生成績的頻率分布直方圖和女生成績的莖葉圖,規定80分以上為優分(含80分).

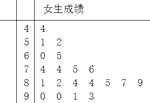
(Ⅰ)(i)請根據圖示,將2×2列聯表補充完整;
優分 | 非優分 | 總計 | |
男生 | |||
女生 | |||
總計 | 50 |
(ii)據此列聯表判斷,能否在犯錯誤概率不超過10%的前提下認為“該學科成績與性別有關”?
(Ⅱ)將頻率視作概率,從高三年級該學科成績中任意抽取3名學生的成績,求至少2名學生的成績為優分的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com