
【題目】某商店計劃每天購進某商品若干件,商店每銷售一件該商品可獲利潤60元,若供大于求,剩余商品全部退回,但每件商品虧損10元;若供不應(yīng)求,則從外部調(diào)劑,此時每件調(diào)劑商品可獲利40元.
(1)若商品一天購進該商品10件,求當(dāng)天的利潤![]() (單位:元)關(guān)于當(dāng)天需求量
(單位:元)關(guān)于當(dāng)天需求量![]() (單位:件,
(單位:件,![]() )的函數(shù)解析式;
)的函數(shù)解析式;
(2)商店記錄了50天該商品的日需求量![]() (單位:件,
(單位:件,![]() ),整理得下表:
),整理得下表:

若商店一天購進10件該商品,以50天記錄的各需求量的頻率作為各需求量發(fā)生的概率,求當(dāng)天的利潤在區(qū)間![]() 內(nèi)的概率.
內(nèi)的概率.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)根據(jù)題意分![]() 和
和![]() 兩段,求分段函數(shù);
兩段,求分段函數(shù);
(2)根據(jù)表格計算不同的日需求量對應(yīng)的利潤,并且計算利潤在![]() 時,對應(yīng)的頻數(shù),并計算頻率,就是所求概率.
時,對應(yīng)的頻數(shù),并計算頻率,就是所求概率.
解:(1)當(dāng)日需求量![]() 時,利潤為
時,利潤為![]() ;
;
當(dāng)日需求量![]() 時,利潤為
時,利潤為![]() .
.
所以利潤![]() 關(guān)于需求量
關(guān)于需求量![]() 的函數(shù)解析式為
的函數(shù)解析式為
![]() .
.
(2)50天內(nèi)有4天獲得的利潤為390元,有8天獲得的利潤為460元,有10天獲得的利潤為530元,有14天獲得的利潤為600元,有9天獲得的利潤為640元,有5天獲得的利潤為680元. 若利潤在區(qū)間![]() 內(nèi),日需求量為9、10、11,其對應(yīng)的頻數(shù)分別為10、14、9. 則利潤在區(qū)間
內(nèi),日需求量為9、10、11,其對應(yīng)的頻數(shù)分別為10、14、9. 則利潤在區(qū)間![]() 內(nèi)的概率為
內(nèi)的概率為![]()


科目:高中數(shù)學(xué) 來源: 題型:
【題目】11月,2019全國美麗鄉(xiāng)村籃球大賽在中國農(nóng)村改革的發(fā)源地-安徽鳳陽舉辦,其間甲、乙兩人輪流進行籃球定點投籃比賽(每人各投一次為一輪),在相同的條件下,每輪甲乙兩人在同一位置,甲先投,每人投一次球,兩人有1人命中,命中者得1分,未命中者得-1分;兩人都命中或都未命中,兩人均得0分,設(shè)甲每次投球命中的概率為![]() ,乙每次投球命中的概率為
,乙每次投球命中的概率為![]() ,且各次投球互不影響.
,且各次投球互不影響.
(1)經(jīng)過1輪投球,記甲的得分為![]() ,求
,求![]() 的分布列;
的分布列;
(2)若經(jīng)過![]() 輪投球,用
輪投球,用![]() 表示經(jīng)過第
表示經(jīng)過第![]() 輪投球,累計得分,甲的得分高于乙的得分的概率.
輪投球,累計得分,甲的得分高于乙的得分的概率.
①求![]() ;
;
②規(guī)定![]() ,經(jīng)過計算機計算可估計得
,經(jīng)過計算機計算可估計得![]() ,請根據(jù)①中
,請根據(jù)①中![]() 的值分別寫出a,c關(guān)于b的表達式,并由此求出數(shù)列
的值分別寫出a,c關(guān)于b的表達式,并由此求出數(shù)列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,且
,且![]() 存在單調(diào)遞減區(qū)間,求實數(shù)
存在單調(diào)遞減區(qū)間,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)函數(shù)![]() 的圖象
的圖象![]() 與函數(shù)
與函數(shù)![]() 的圖象
的圖象![]() 交于點
交于點![]() ,
, ![]() ,過線段
,過線段![]() 的中點作
的中點作![]() 軸的垂線分別交
軸的垂線分別交![]() ,
, ![]() 于點
于點![]() ,
, ![]() ,證明:
,證明: ![]() 在點
在點![]() 處的切線與
處的切線與![]() 在點
在點![]() 處的切線不平行.
處的切線不平行.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的半焦距為
的半焦距為![]() ,圓
,圓![]() 與橢圓
與橢圓![]() 有且僅有兩個公共點,直線
有且僅有兩個公共點,直線![]() 與橢圓
與橢圓![]() 只有一個公共點.
只有一個公共點.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)已知動直線![]() 過橢圓
過橢圓![]() 的左焦點
的左焦點![]() ,且與橢圓
,且與橢圓![]() 分別交于
分別交于![]() 兩點,試問:
兩點,試問:![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 為定值?若存在,求出該定值和點
為定值?若存在,求出該定值和點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國古代十進制的算籌計數(shù)法,在數(shù)學(xué)史上是一個偉大的創(chuàng)造,算籌實際上是一根根同長短的小木棍.如圖,是利用算籌表示1-9的一種方法.則據(jù)此,3可表示為“![]() ”,26可表示為“
”,26可表示為“![]() ”,現(xiàn)有6根算籌,據(jù)此表示方法,若算籌不能剩余,則可以用1-9這9數(shù)字表示的兩位數(shù)的個數(shù)為( )
”,現(xiàn)有6根算籌,據(jù)此表示方法,若算籌不能剩余,則可以用1-9這9數(shù)字表示的兩位數(shù)的個數(shù)為( )
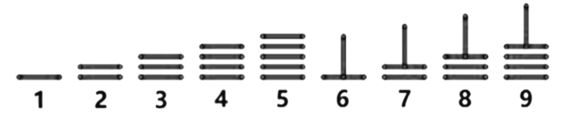
A.9B.13C.16D.18
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在矩形PABC中,AB=2BC=4,D為PC的中點,以AD為折痕將△PAD折起,折到如圖2的位置,使得PB=2![]() .
.

(1)求證:AP⊥平面PBD
(2)求平面PCD與平面PBC所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ),
),![]() 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(1)當(dāng)![]() 時,求
時,求![]() 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(2)若對任意的![]() ,
,![]() (
(![]() ),求
),求![]() 的最大值;
的最大值;
(3)若![]() 的極大值為
的極大值為![]() ,求不等式
,求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=a(x﹣1)﹣lnx(a∈R),g(x)=(1﹣x)ex.
(1)討論函數(shù)f(x)的單調(diào)性;
(2)若對任意給定的x0∈[﹣1,1],在區(qū)間(0,e]上總存在兩個不同的xi(i=1,2),使得f(xi)=g(x0)成立,求a的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com