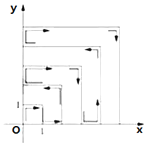
【題目】如圖,一個粒子的起始位置為原點,在第一象限內(nèi)于兩正半軸上運動,第一秒運動到(0,1),而后它接著按圖示在
軸、
軸的垂直方向來回運動,且每秒移動一個單位長度,如圖所示,經(jīng)過
秒時移動的位置設為
,那么經(jīng)過2019秒時,這個粒子所處的位置的坐標是______.
優(yōu)翼小幫手同步口算系列答案科目：高中數(shù)學 來源： 題型：
【題目】橢圓C：
過點M（2，0），且右焦點為F（1，0），過F的直線l與橢圓C相交于A、B兩點．設點P（4，3），記PA、PB的斜率分別為k1和k2．
（1）求橢圓C的方程；
（2）如果直線l的斜率等于-1，求出k1k2的值；
（3）探討k1+k2是否為定值？如果是，求出該定值；如果不是，求出k1+k2的取值范圍．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的左．右焦點分別為
,短軸兩個端點為
,且四邊形
的邊長為
的正方形．
（Ⅰ）求橢圓的方程；
（Ⅱ）若
,分別是橢圓長軸的左,右端點,動點
滿足
,連結
,交橢圓于點
．證明: 
的定值；
（Ⅲ）在（Ⅱ）的條件下,試問
軸上是否存在異于點
,的定點
,使得以
為直徑的圓恒過直線
,
的交點,若存在,求出點的坐標；若不存在,說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某老師是省級課題組的成員，主要研究課堂教學目標達成度，為方便研究，從實驗班中隨機抽取30次的隨堂測試成績進行數(shù)據(jù)分析
已知學生甲的30次隨堂測試成績?nèi)缦?/span>
滿分為100分
：
88 58 50 36 75 39 57 62 72 51
85 39 57 53 72 46 64 74 53 50
44 83 70 63 71 64 54 62 61 42
把學生甲的成績按
，
，
，
，
，
分成6組，列出頻率分布表，并畫出頻率分布直方圖；
為更好的分析學生甲存在的問題，從隨堂測試成績50分以下不包括50分的試卷中隨機抽取3份進行分析，求恰有2份成績在內(nèi)的概率．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，正方體
的棱長為1，線段
上有兩個動點
，且
，現(xiàn)有如下四個結論：
；
平面
；
三棱錐
的體積為定值；
異面直線
所成的角為定值，
其中正確結論的序號是______．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知等比數(shù)列
滿足：
，
．
（1）求數(shù)列的通項公式；
（2）是否存在正整數(shù)
，使得
？若存在，求的最小值；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖是某地區(qū)2012年至2018年生活垃圾無害化處理量（單位：萬噸）的折線圖.
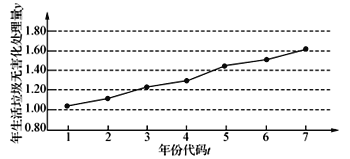
注：年份代碼
分別表示對應年份
.
（1）由折線圖看出，可用線性回歸模型擬合
與
的關系，請用相關系數(shù)
（
線性相關較強）加以說明；
（2）建立與的回歸方程(系數(shù)精確到0.01)，預測2019年該區(qū)生活垃圾無害化處理量.
（參考數(shù)據(jù)）
，
，
，
，
，
，
.
（參考公式）相關系數(shù)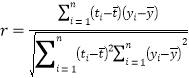
，在回歸方程
中斜率和截距的最小二乘估計公式分別為：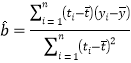
，
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點
為雙曲線
: 
的左、右焦點，過
作垂直于
軸的直線，在軸上方交雙曲線C于點
，且
（1）求雙曲線C的方程；
（2）若直線
與雙曲線C恒有兩個不同交點P和Q且
（其中O為原點），求k的取值范圍;
（3）過雙曲線C上任意一點R作該雙曲線兩條漸近線的垂線，垂足分別為M,N，求
的值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知過點
的動直線
與圓
：
相交于
、
兩點，
是
中點，與直線
：
（
為常數(shù)）相交于點
.
（1）求證：當與垂直時，必過圓心；
（2）當
時，求直線的方程；
（3）當直線的傾斜角
變化時，探索
的值是否為常數(shù)？若是，求出該常數(shù)；若不是，請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
