【題目】某公司為評估兩套促銷活動方案（方案1運作費用為5元/件；方案2的運作費用為2元/件），在某地區部分營銷網點進行試點（每個試點網點只采用一種促銷活動方案），運作一年后，對比該地區上一年度的銷售情況，制作相應的等高條形圖如圖所示．
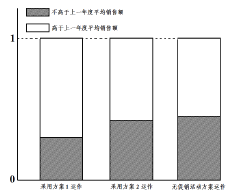
（1）請根據等高條形圖提供的信息，為該公司今年選擇一套較為有利的促銷活動方案（不必說明理由）；
（2）已知該公司產品的成本為10元/件（未包括促銷活動運作費用），為制定本年度該地區的產品銷售價格，統計上一年度的8組售價
（單位：元/件，整數）和銷量
（單位：件）（
）如下表所示：
售價 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
銷量 | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
①請根據下列數據計算相應的相關指數
，并根據計算結果，選擇合適的回歸模型進行擬合；
②根據所選回歸模型，分析售價
定為多少時？利潤
可以達到最大.
|
|
| |
| 49428.74 | 11512.43 | 175.26 |
| 124650 | ||
（附：相關指數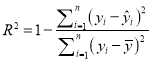
）
【答案】（1）年度平均銷售額與方案1的運作相關性強于方案2.（2）①采用回歸模型
進行擬合最為合適. ②
【解析】試題分析：（1）由等高條形圖可判斷年度平均銷售額與方案1的運作相關性強于方案2.
（2）①由已知數據可知， 
比較大小可得最佳擬合方案;
②由（1）可知，采用方案1的運作效果較方案2好，故年利潤
，求導求最值即可.
試題解析：（1）由等高條形圖可知，年度平均銷售額與方案1的運作相關性強于方案2.
（2）①由已知數據可知，回歸模型
對應的相關指數
；
回歸模型
對應的相關指數
；
回歸模型
對應的相關指數
.
因為
，所以采用回歸模型
進行擬合最為合適.
②由（1）可知，采用方案1的運作效果較方案2好，
故年利潤
， 
，
當
時， 
單調遞增；
當
時， 
單調遞減，
故當售價
時，利潤達到最大.
科目：高中數學 來源： 題型：
【題目】對于無窮數列
，記
，若數列
滿足：“存在
，使得只要
（
且
），必有
”，則稱數列
具有性質
.
（Ⅰ）若數列
滿足
判斷數列
是否具有性質
？是否具有性質
？
（Ⅱ）求證：“
是有限集”是“數列
具有性質
”的必要不充分條件；
（Ⅲ）已知
是各項為正整數的數列，且
既具有性質
，又具有性質
，求證：存在整數
，使得
是等差數列.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2， 
.
（1）求證：PD⊥平面PAB；
（2）求直線PB與平面PCD所成角的正弦值.
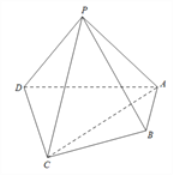
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列4個命題，其中正確的命題序號為（ ）
①|x+ 
|的最小值是2 ② 
的最小值是2 ③log2x+logx2的最小值是2 ④3x+3﹣x的最小值是2．
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在等腰梯形
中， 
， 
， 
，四邊形
為矩形， 
，平面
平面
，點
為線段
中點．
（Ⅰ）求異面直線
與
所成的角的正切值；
（Ⅱ）求證：平面
平面
；
（Ⅲ）求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
.
（1）若橢圓
的右焦點坐標為
，求
的值；
（2）由橢圓
上不同三點構成三角形稱為橢圓的內接三角形.若以
為直角頂點的橢圓
的內接等腰直角三角形恰有三個，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面
是矩形，面
底面
，且
是邊長為
的等邊三角形， 
， 
在
上，且
∥面BDM.
（1）求直線PC與平面BDM所成角的正弦值；
（2）求平面BDM與平面PAD所成銳二面角的大小.
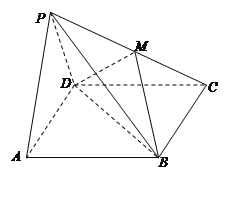
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
